Die Tauschökonomie
In einer Vorlesung zur Mikroökonomie ist die Analyse einer Tauschökonomie aus zwei Konsumenten in der Regel der erste Schritt in Richtung allgemeiner Gleichgewichtstheorie. Dieser Schritt von der partiellen zur allgemeinen Gleichgewichtsanalyse ist größer als er auf den ersten Blick erscheint, denn Preise und Einkommen sind fortan nicht mehr exogen gegeben, sondern bestimmen sich aus dem Marktgeschehen. Die Entscheidung des einen hängt von der Entscheidung des anderen ab. Dadurch ist die Mathematik des Gleichgewichts anderer Art als man es aus der partiellen Analyse gewohnt ist, und es gilt gleich zu Anfang sowohl mathematisch als auch ökonomisch Grundlegendes in der Tauschökonomie zweier Konsumenten zu verstehen.
Als ich in I. M. D. Littles großartiger Dissertation A Critique of Welfare Economics
eine Edgeworth-Box mathematisch nachvollziehen wollte, mußte ich mir Defizite im mathematischen und ökonomischen Verständnis eingestehen und mein Wissen über das Konzept der Tauschökonomie nicht nur auffrischen, sondern vertiefen und ergänzen. Dies ist der Anlaß für diesen Artikel. Das Ziel ist, die für die Mikroökonomik zentrale Theorie des Allgemeinen Gleichgewichts bis zum Ersten Hauptsatz der Wohlfahrtsökonomik anhand des einfachen Falles einer Tauschökonomie mit zwei Personen und zwei Gütern so darzustellen, dass man für den Kern der Theorie ein Verständnis gewinnen kann, mit dem sich alle darüber hinausgehenden Inhalte leichter erschließen. Ich hoffe, diese Darstellung ist für manche Studentinnen und Studenten der Wirtschaftswissenschaften erhellend. Dem ökonomisch interessierten Laien bietet der Artikel Grundbegriffe der Mikroökonomik
eine propädeutische Einführung in die hier vorausgesetzen Begrifflichkeiten und Konzepte.
Inhalt
1. Das mathematische Modell
2. Marktgleichgewicht und Pareto-Effizienz
3. Die Grenzrate der Substitution und Pareto-Effizienz
4. Die Herleitung der Kontraktkurve
5. Individuelle Nutzenmaximierung und Nachfragefunktionen
6. Walras'sches Gesetz, Überschußnachfrage und die Relativität der Preise
7. Das Allgemeine Gleichgewicht
8. Begründung des Marktgleichgewichts
9. Der Erste Hauptsatz der Wohlfahrtsökonomik
10. Exkurs: Edgeworth und die Vollkommenheit der Märkte
11. Abschließende Bemerkungen
Literatur
1. Das mathematische Modell
Wir definieren zu Anfang die Funktionen und Variablen der Tauschökonomie: Es gibt zwei Individuen \(A\) und \(B\), die zwei Güter \(X\) und \(Y\) tauschen. Die Menge, die Individuum \(A\) von Gut \(X\) konsumiert, nennen wir \(x_a\); die Menge, die \(A\) von Gut \(Y\) konsumiert, nennen wir \(y_a\). Für Individuum \(B\) nennen wir diese Gütermengen entsprechend \(x_b\) und \(y_b\). Die Individuen haben die Cobb-Douglas-Nutzenfunktionen $$\begin{aligned} U_a(x_a, y_a) \; &= \; x_a^\alpha \; y_a^{(1-\alpha)} \qquad \text{mit } \alpha \in [0;1]\\[0.5em] U_b(x_b, y_b) \; &= \; x_b^\beta \; y_b^{(1-\beta)} \qquad \text{mit } \beta \in [0;1] \end{aligned}$$
In der Ökonomie ist insgesamt die Menge \(\omega^x\) an Gut \(X\) und die Menge \(\omega^y\) an Gut \(Y\) vorhanden. Individuum \(A\) verfügt am Anfang über \(\omega^x_a\) Einheiten von Gut \(X\) und über \(\omega^y_a\) Einheiten von Gut \(Y\). Die Anfangsausstattung von Individuum \(B\) nennen wir entsprechend \(\omega^x_b\) und \(\omega^y_b\). Den Punkt der Anfangsverteilung in der Edgeworth-Box nennen wir \(\Omega\). Beachte, dass die Ausstattungen exogen gegeben sind, während die konsumierten Mengen \(x_a\), \(x_b\), \(y_a\) und \(y_b\) endogene Variablen sind.
In der Tauschökonomie findet keine Produktion statt und es werden keine Güter weggeworfen. Es gilt daher als Feasibility-Bedingung: $$\begin{aligned} \omega^x \; &= \; \omega^x_a \,+\, \omega^x_b \; = \; x_a \,+\, x_b\\[0.5em] \omega^y \; &= \; \omega^y_a \,+\, \omega^y_b \; = \; y_a \,+\, y_b \end{aligned}$$
Die folgende Edgeworth-Box macht diese Definitionen anschaulich:
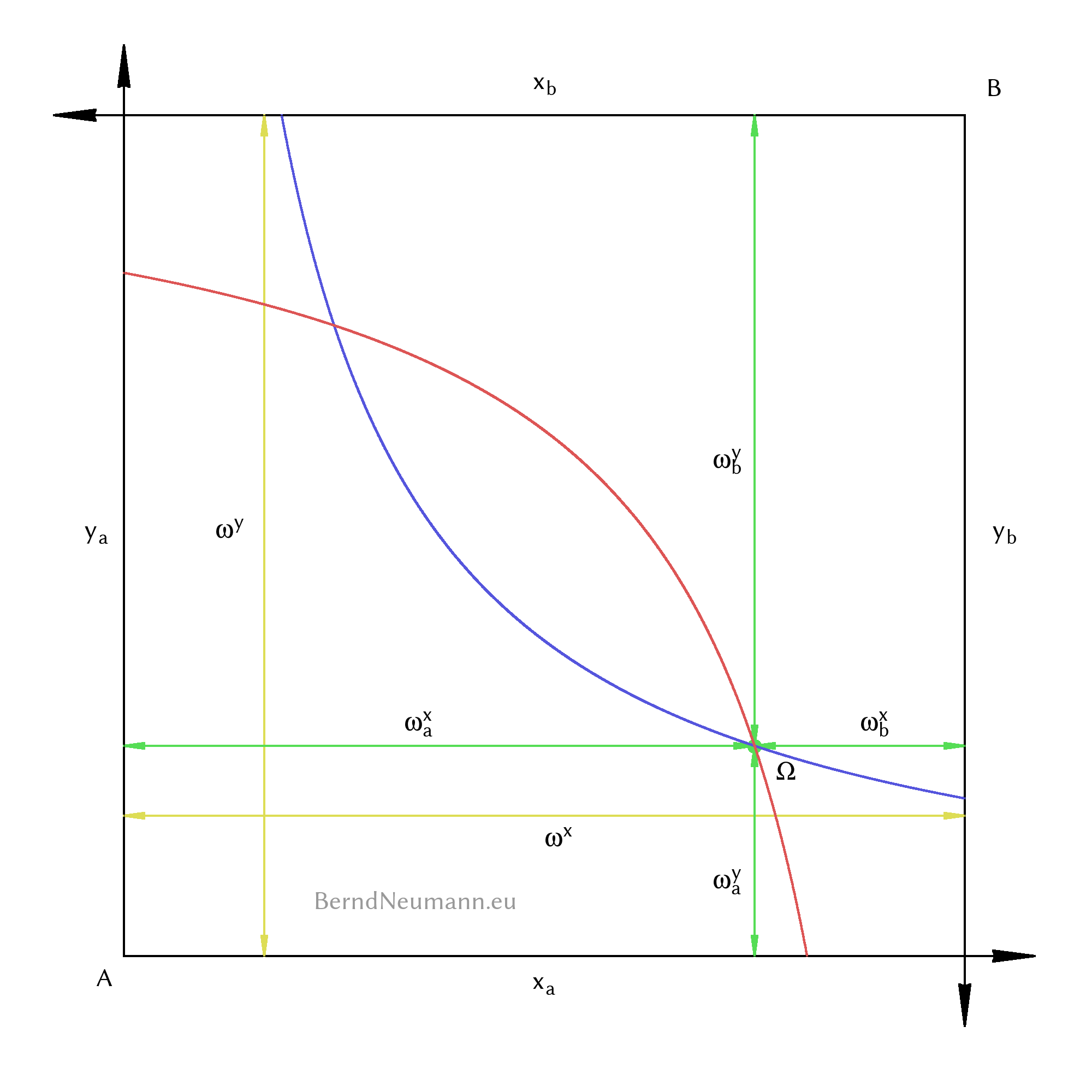
2. Marktgleichgewicht und Pareto-Effizienz
In der Edgeworth-Box einer Tauschökonomie werden zwei Konzepte dargestellt. Auf der einen Seite gibt es Märkte, auf denen Güter zu bestimmten Preisen angeboten und nachgefragt werden. Sind auf allen Märkten Angebot und Nachfrage gleich, sprechen wir von einem Allgemeinen Gleichgewicht. Dieser Teil der Theorie beschreibt das Resultat des individuellen Handelns auf den Märkten. Auf der anderen Seite steht die Pareto-Effizienz. Eine Allokation ist pareto-effizient, wenn man niemanden besser stellen kann ohne einen anderen schlechter zu stellen. Anders gesagt verschwendet man bei einer pareto-effizienten Allokation nicht die Möglichkeit, durch Tausch die Wohlfahrt der Menschen zu verbessern. Dieser Teil der Theorie erklärt, welche Allokationen wünschenswert sind.
Es ist wichtig, diese beiden Teile deutlich zu unterscheiden. Das mag in einer Tauschökonomie mit nur zwei Personen und zwei Gütern nebensächlich oder gar unrealistisch erscheinen, aber es geht nicht darum, das Handeln von zwei Personen auf einer einsamen Insel mit zwei Gütern zu erklären, sondern der einfache Zwei-Personen-Fall steht für Märkte mit vielen Teilnehmern, die unter vollkommener Konkurrenz agieren. Wie beide Teile zusammenhängen ist die Pointe am Ende in Form des Ersten Hauptsatzes der Wohlfahrtsökonomik. Er wird gegenstandslos, wenn man die Teile vorher unachtsam vermischt.
In den folgenden Abschnitten werde ich nacheinander beide Konzepte erläutern. Dabei geht es nicht darum, auf möglichst kurzem und direktem Weg zum ersten Hauptsatz der Wohlfahrtsökonomik zu gelangen, sondern die Mathematik und ihre ökonomische Bedeutung ausführlich zu erklären und mit entsprechenden Grafiken zu veranschaulichen. Wir beginnen mit den pareto-effizienten Allokationen, indem wir in der Edgeworth-Box die Bedeutung der Grenzrate der Substitution untersuchen.
3. Die Grenzrate der Substitution und Pareto-Effizienz
In der partiellen Gleichgewichtsanalyse ist es ebenso anschaulich wie hinreichend, die Grenzrate der Substitution als Steigung der Indifferenzkurven zu verstehen. Für die allgemeine Gleichgewichtsanalyse ist es anschaulicher, sie wie die Nutzenfunktionen als ein Skalarfeld zu denken. Statt des Nutzenwertes liefert die Funktion der Grenzrate der Substitution zu jeder Allokation einen Skalar, der die Tauschbereitschaft ausdrückt. Tauschbereitschaft heißt, dass man für eine marginale Einheit eines Gutes bereit ist, höchstens eine bestimmte Menge des anderen Gutes herzugeben. Leiten wir uns diese Anschauung von Anfang an her: Wir haben die Nutzenfunktionen, die wir als Indifferenzkurven in die Edgeworth-Box zeichnen. In Wirklichkeit ist die Nutzenfunktion dreidimensional, und die Indifferenzkurven sind ihre Höhenlinien in der zweidimensionalen Edgeworth-Box. Liegt ein Tausch auf einer Höhenlinie und entspricht somit genau der Tauschbereitschaft, bleibt das Nutzeniveau konstant. Die Nutzendifferenz vor und nach dem Tausch ist null: $$\begin{aligned} \Delta U(x, y) \; &= \; 0 \end{aligned}$$
Damit das erfüllt ist, muß bei einem Tausch folgendes passieren: Man bekommt von einem Gut, sagen wir es sei Gut \(X\), eine marginale Einheit \({\text d}x\) dazu. Durch diese Bewegung in \(x\)-Richtung verändert sich der Nutzen entsprechend der Steigung in dieser Richtung. Diese Steigung der Nutzenfunktion ist ihre partielle Ableitung nach \(x\). Damit \(\Delta U\) null bleibt, müssen wir diesen Nutzengewinn durch eine entsprechende Bewegung \({\text d}y\) ausgleichen. Diese Bewegung in \(y\)-Richtung muß mit der Steigung der Nutzenfunktion in \(y\)-Richtung gewichtet werden. Die Summe dieser beiden Bewegungen, die wir in einfacher Plus-Minus-Arithmetik überlegt haben, ist das totale Differential der Nutzenfunktion \(\Delta U(x, y)\): $$\begin{aligned} \Delta U(x, y) \; = \; \frac{\partial U(x, y)}{\partial x}{\text d}x \; + \; \frac{\partial U(x, y)}{\partial y}{\text d}y \; &= \; 0 \end{aligned}$$
Durch Umformen erhält man: $$\begin{aligned} \frac{{\text d}y}{{\text d}x} \; &= \; -\frac{\frac{\partial U(x, y)}{\partial x}}{\frac{\partial U(x, y)}{\partial y}} \end{aligned}$$
Der linke Teil dieser Gleichung liest sich wie folgt: Damit der Nutzen konstant bleibt, \(\Delta U = 0\), muß sich \(y\) um \({\text d}y\) ändern, wenn sich \(x\) um \({\text d}x\) ändert. Auf der rechten Seite der Gleichung stehen die partiellen Ableitungen, die aufgrund der Monotonie immer positiv sind. Durch das Minuszeichen ist der rechte Teil immer negativ. Das bedeutet, dass auf der linken Seite \({\text d}x\) und \({\text d}y\) verschiedene Vorzeichen haben müssen. Das heißt ökonomisch, dass man bereit ist, von Gut \(Y\) etwas herzugeben, wenn man eine marginale Einheit von Gut \(X\) dazu bekommt und der Nutzen konstant bleiben soll. Diese Menge, die man von Gut \(Y\) hergeben würde, ist die (negative) Steigung der Indifferenzkurve und nichts anderes als die Grenzrate der Substitution.
Wir nennen die Grenzrate der Substitution \(\text{GRS}^x\) und schreiben sie als Funktion \(\text{GRS}^x(x, y)\). Der hochgestellte Index \(x\) erinnert daran, dass wir das totale Differential zu \(\frac{{\text d}y}{{\text d}x}\) umgeformt haben. Die Tauschbereitschaft als Einheiten von Gut \(Y\) pro Einheit von Gut \(X\) auszudrücken ist willkürlich, denn wir hätten auch zu \(\frac{{\text d}x}{{\text d}y}\) umformen können. Wichtig ist, sich für ein Bezugsgut zu entscheiden und für alle Individuen beizubehalten. Mit der Gleichung aus dem totalen Differential können wir die Funktion der Grenzrate der Substitution für beide Individuen berechnen, indem wir die partiellen Ableitungen bilden und einsetzen: $$\begin{aligned} \text{GRS}_a^x(x_a, y_a) \; &= \; -\;\frac{\alpha x_a^{(\alpha-1)}y_a^{(1-\alpha)}}{x_a^\alpha (1-\alpha)y_a^{(1-\alpha-1)}}\\[1em] \text{GRS}_a^x(x_a, y_a) \; &= \; -\; \frac{\alpha}{1-\alpha} \frac{y_a}{x_a}\\[1em] \text{GRS}_b^x(x_b, y_b) \; &= \; -\; \frac{\beta}{1-\beta} \frac{y_b}{x_b} \end{aligned}$$
Mit den Gleichungen für die Grenzrate der Substitution können wir die Optimalbedingung für die pareto-effizienten Allokationen formulieren. Eine Allokation ist pareto effizient, wenn niemand besser gestellt werden kann, ohne dafür jemand anderen schlechter zu stellen. Das ist der Fall, wenn die Grenzrate der Substitution beider Individuen gleich ist. Denn angenommen sie wäre nicht gleich, dann wäre einer von beiden bereit, mehr Gut \(Y\) für eine marginale Einheit von Gut \(X\) zu bezahlen als der andere benötigt, um bei konstantem Nutzenniveau eine marginale Einheit Gut \(X\) zu geben. Mit dieser Differenz könnte man einen oder beide besser stellen, so dass die Ausgangsallokation nicht pareto-effizient gewesen sein kann.
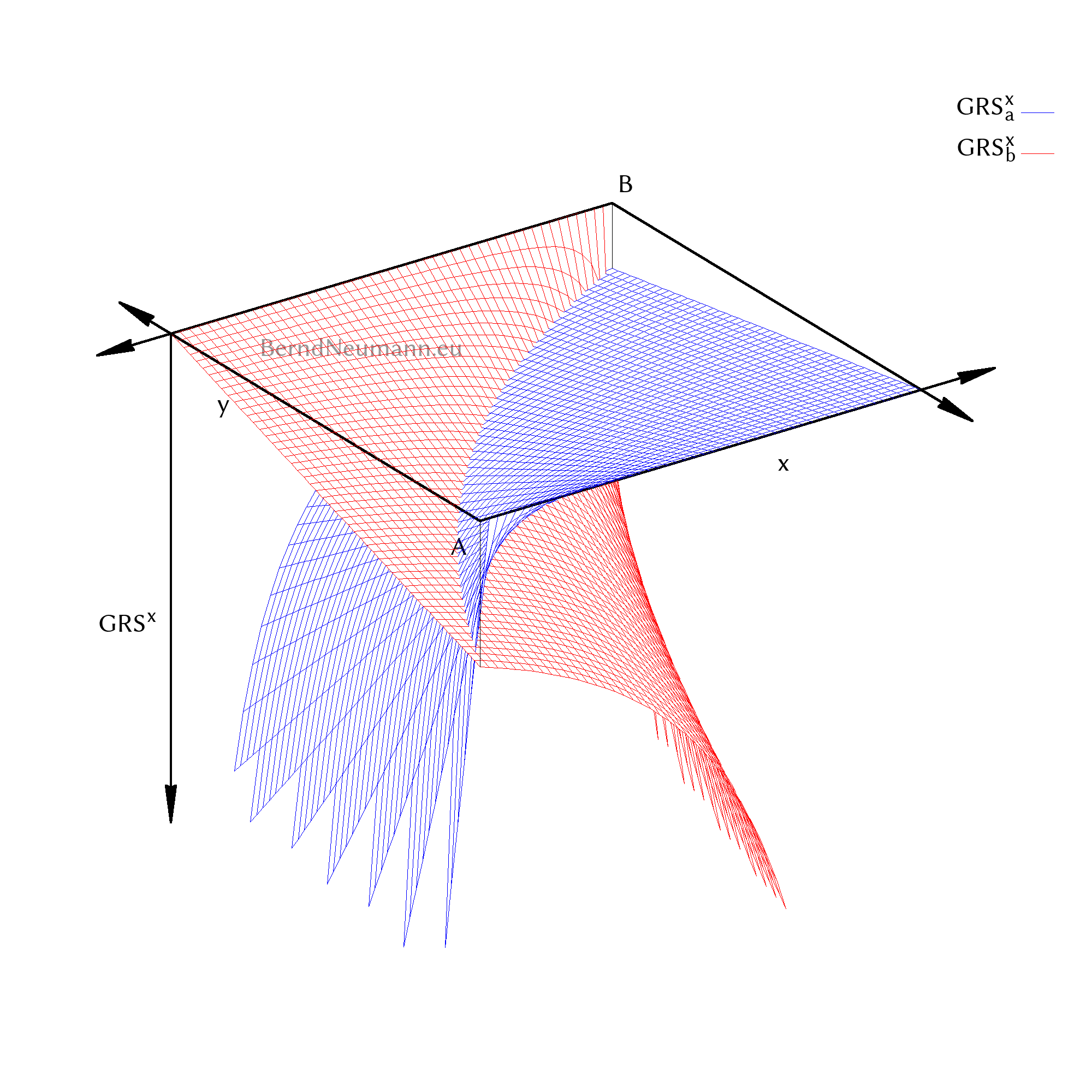
Die beiden folgenden Abbildungen illustrieren diesen Zusammenhang mit \(\alpha = \frac{2}{5}\) und \(\beta = \frac{3}{5}\). Dabei liefert Abbildung 3a die mathematisch intuitive Anschauung, indem sie die \(\text{GRS}^x\) als ein Skalarfeld darstellt, das die Tauschbereitschaft ausdrückt. Abbildung 3b entspricht der gewohnten ökonomischen Anschauung. In ihr zeigt die linsenförmige gemeinsame Bessermenge die Möglichkeit, mindestens einen besser zu stellen, ohne dafür den anderen schlechter stellen zu müssen. Nur wenn sich die Indifferenzkurven gerade berühren, also ihre Steigungen, mithin die Grenzrate der Substitution beider Individuen, für eine Allokation gleich sind, ist eine pareto-effiziente Verteilung erreicht.
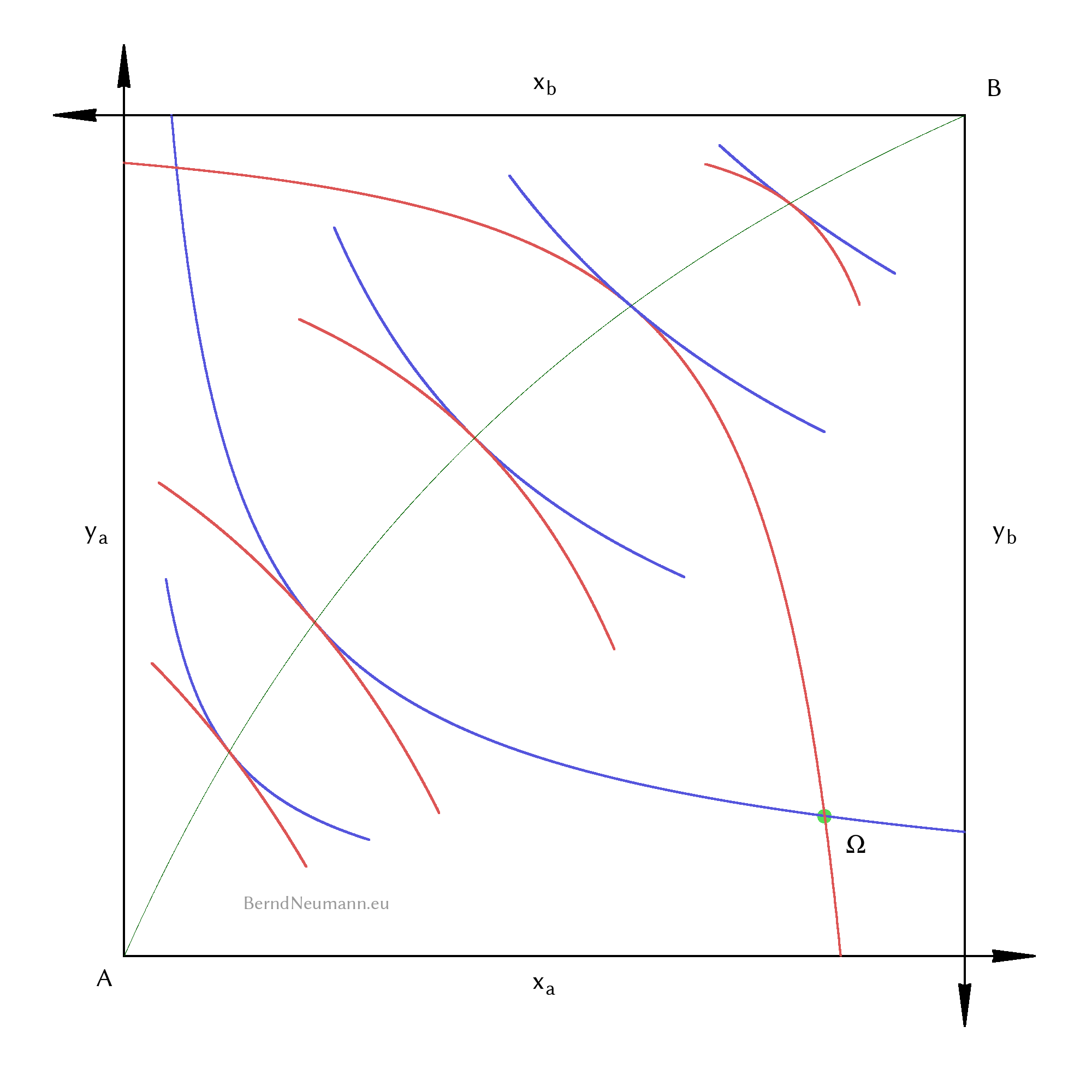
Point on the Contract Curve.
Beide Darstellungen zeigen das Offensichtliche: Bei pareto-effizienten Allokationen ist die Grenzrate der Substitution der Individuen gleich. Dabei haben beide Darstellungen Vor- und Nachteile. Die übliche Darstellung mit den Indifferenzkurven macht deutlich, ob man jemanden besserstellen kann oder nicht. Damit wird die ökonomische Bedeutung der Pareto-Effizienz anschaulich, auf die wir mit der Grenzrate der Substitution hinaus möchten. Jedoch tritt dabei die mathematische Anschauung in den Hintergrund. Der Blick auf die Indifferenzkurven und ihre Steigung verschleiert, dass die Grenzrate der Substitution eine Funktion ist, die für eine bestimmte Allokation die Tauschbereitschaft des Individuums ausdrückt. Diese mathematische Anschauung ist klarer, wenn man die Grenzrate der Substitution als Funktion schreibt und dreidimensional als Skalarfeld darstellt.
4. Die Herleitung der Kontraktkurve
Wir suchen die Menge der pareto-effizienten Allokationen und möchten dafür die Gleichung der Kontraktkurve herleiten. Im vorherigen Abschnitt haben wir die \(\text{GRS}^x\) für beide Individuen ausgerechnet und gezeigt, dass in pareto-effizienten Allokationen die Grenzraten der Substitution gleich sein müssen. Gleichsetzen und Einsetzen ergibt: $$\begin{aligned} \text{GRS}_a^x(x_a, y_a) \; &= \; \text{GRS}_b^x(x_b, y_b)\\[1em] \frac{\alpha}{1-\alpha} \frac{y_a}{x_a} \; &= \; \frac{\beta}{1-\beta} \frac{y_b}{x_b} \end{aligned}$$
Wir haben jetzt eine Gleichung mit vier variablen Gütermengen. Sie sagt uns, für welche Güterbündel \((x_a; y_a)\) und \((x_b; y_b)\) die Grenzrate der Substitution beider Individuen gleich ist. Jedoch enthält diese Gleichung nichts, das sie auf mögliche Allokationen der Edgeworth-Box beschränkt. Stattdessen formuliert sie eine Beziehung zwischen Güterbündeln in den zwei voneinander unabhängigen Koordinatensystemen der Gütermengendiagramme von Individuum \(A\) und Individuum \(B\). Um von dieser Gleichung eine mathematische Anschauung zu gewinnen, müssen wir daher die Edgeworth-Box verlassen und die Gleichung in zwei unabhängigen Gütermengendiagrammen darstellen.
In beiden Gütermengendiagrammen liegen alle Punkte mit der gleichen Grenzrate der Substitution auf einer Ursprungsgeraden und zu einer bestimmten \(\text{GRS}^x\) gehört je eine Gerade. Die zugehörigen Geradengleichungen erhält man, indem man die \(\text{GRS}^x\)-Funktionen nach \(y_a\) und \(y_b\) umformt und die \(\text{GRS}^x\) als Parameter auffaßt. Erinnern wir uns an die dreidimensionale Darstellung der \(\text{GRS}\) als Skalarfeld in Abbildung 3a, dann repräsentieren diese Geraden als Iso-GRS-Linien
dieses Skalarfeld wie die zweidimensionalen Indifferenzkurven die dreidimensionale Nutzenfunktion repräsentieren. Dass die Linien gleicher \(\text{GRS}\) Geraden sind, ist eine Eigenschaft der Cobb-Douglas-Präferenzen. Die Steigung der Geraden hängt von den Präferenzen und der \(\text{GRS}^x\) ab. Je stärker das Individuum Gut \(Y\) präferiert, desto größer ist ihre Steigung und sie verläuft näher an der Achse für Gut \(Y\). Ebenso verläuft die Gerade für kleinere, vom Betrag her größere, \(\text{GRS}^x\) steiler, und für größere, vom Betrag her kleinere, flacher und näher an der Achse für Gut \(X\).
Zur Kontraktkurve gelangen wir, indem wir die beiden Gütermengendiagramme aus Abbildung 4a zu einer Edgeworth-Box vereinen. Algebraisch geschieht das mit den Feasibility-Bedingungen. Zusammen mit der Gleichung der Optimalbedingung haben wir dann drei Gleichungen mit vier variablen Gütermengen. Aus diesen drei können wir die Kontraktkurve als eine Gleichung \(y_a(x_a)\) ableiten. Geometrisch drehen wir dafür, anschließend an Abbildung 4a, das Gütermengendiagramm von Individuum \(B\) um 180 Grad und verschieben es so, dass sich die Edgeworth-Box ergibt. Mögliche Güterbündel sind dann ausschließlich gültige Allokationen der Edgeworth-Box und die Optimalbedingung ist dort erfüllt, wo sich Geraden gleicher \(\text{GRS}^x\) oder sich, nach Abbildung 4a, Geraden gleicher Farbe schneiden. Diese Schnittpunkte sind die Punkte der Kontraktkurve.

Point on the Contract Curve.
Für die algebraische Lösung setzen wir die Feasibility-Bedingungen in die Gleichung der Optimalbedingung ein: $$\begin{aligned} \frac{\alpha}{1-\alpha} \frac{y_a}{x_a} \; &= \; \frac{\beta}{1-\beta} \frac{(\omega^y-y_a)}{(\omega^x-x_a)} \end{aligned}$$
Das formen wir nach \(y_a\) um und erhalten die Menge der pareto-effizienten Allokationen als Gleichung der Kontraktkurve: $$\begin{aligned} y_a \; &= \; \frac{(1-\alpha)\beta \omega^y x_a}{\alpha\,(1-\beta)\,\omega^x \; - \; \alpha\,(1-\beta)\,x_a \; + \; (1-\alpha)\beta x_a} \end{aligned}$$
Für diese Herleitung sind wir sehr detailliert auf die mathematische Anschauung eingegangen, weil der Rechenweg sonst leicht kontra-intuitiv ist: Wir zeichnen gewöhnlich zuerst die Edgeworth-Box und dann, wie in Abbildung 3b geschehen, sich berührende Indifferenzkurven, rechnen aber in umgekehrter Reihenfolge, indem wir zuerst die Grenzraten der Substitution gleichsetzen und dann die Allokationen mit den Feasibility-Bedingungen auf die Edgeworth-Box beschränken. Durch diese detaillierte Darstellung sollte klar geworden sein, dass drei Schritte erforderlich sind, um zur Kontraktkurve zu gelangen, und jeder Schritt entspricht einer eigenen mathematischen Anschauung und hat eine eigene ökonomische Bedeutung. Man muß
- die Funktionen der Grenzrate der Substitution bestimmen;
- die Güterbündel auf solche mit der gleichen Grenzrate der Substitution einschränken, sprich die Funktionen der Grenzrate der Substitution gleichsetzen;
- die Güterbündel auf die möglichen Allokationen der Edgeworth-Box beschränken, indem man die Feasibility-Bedingung einsetzt und damit alles in dem Koordinatensystem ausdrückt, in das man die Kontraktkurve zeichnen möchte.
Die Reihenfolge spielt keine Rolle: Man kann auch den dritten Schritt vor dem ersten machen und die Feasibility-Bedingungen dafür in die Nutzenfunktion von Individuum \(B\) einsetzen, muß dann aber die partiellen Ableitungen für die \(\text{GRS}^x_b\)-Funktion etwas umständlicher mit der Kettenregel bilden. Die Kontraktkurve als Ergebnis ist in jedem Fall die gleiche. – Ich möchte noch auf einen anderen algebraischen Lösungsweg hinweisen: Dabei maximiert man den Nutzen eines Individuums unter den drei Nebenbedingungen, das andere Individuum habe ein bestimmtes Nutzenniveau und beide Feasibility-Bedingungen seien erfüllt. Dieses Maximierungsproblem kann man mit dem Lagrange-Verfahren lösen und erhält aus den partiellen Ableitungen der Lagrange-Funktion ein Gleichungssystem, das den drei soeben beschriebenen Schritten entspricht. Dieser Weg ist geometrisch anschaulich und elegant, aber auch mathematisch anspruchsvoller, ohne das ökonomische Verständnis zu erweitern. Daher möchte ich es dabei belassen, ihn kurz angedeutet zu haben.
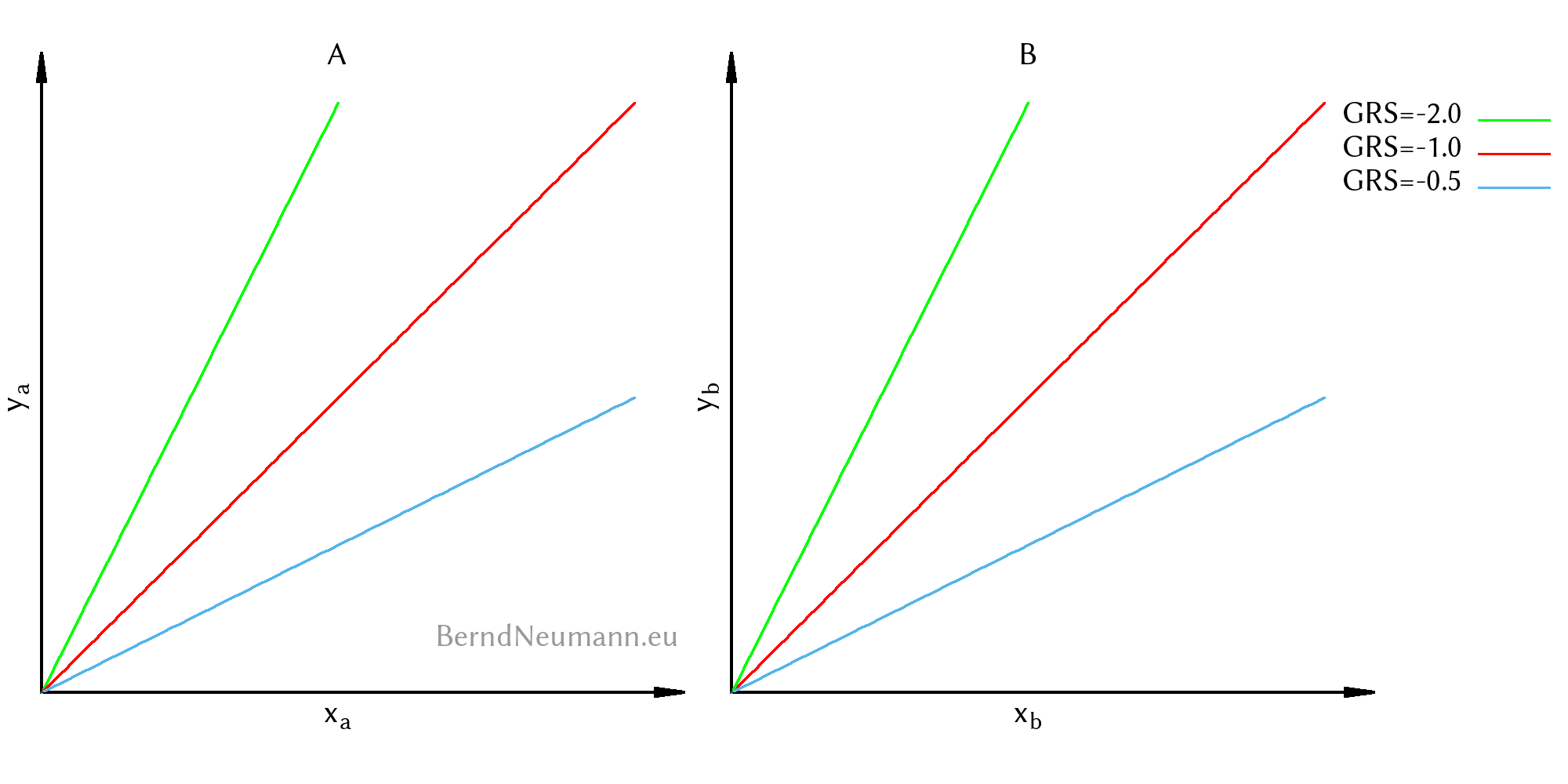
In den Beispiel-Rechnungen der Tutorien kommt als Kontraktkurve meist eine einfache Geradengleichung heraus. Das ist der Fall, wenn beide Individuen die gleichen Präferenzen haben, wenn also für unsere Cobb-Douglas-Nutzenfunktionen \(\alpha=\beta\) gilt. In der Gleichung der Kontraktkurve kürzen sich dann alle \(\alpha\) und \(\beta\) heraus und übrig bleibt eine Gerade mit der Steigung \(\frac{\omega^y}{\omega^x}\). $$\begin{aligned} y_a \; &= \; \frac{\omega^y}{\omega^x}\;x_a \end{aligned}$$
Kontraktkurven für verschiedene Werte von \(\alpha\) und \(\beta\) geben abschließend einen anschaulichen Eindruck:
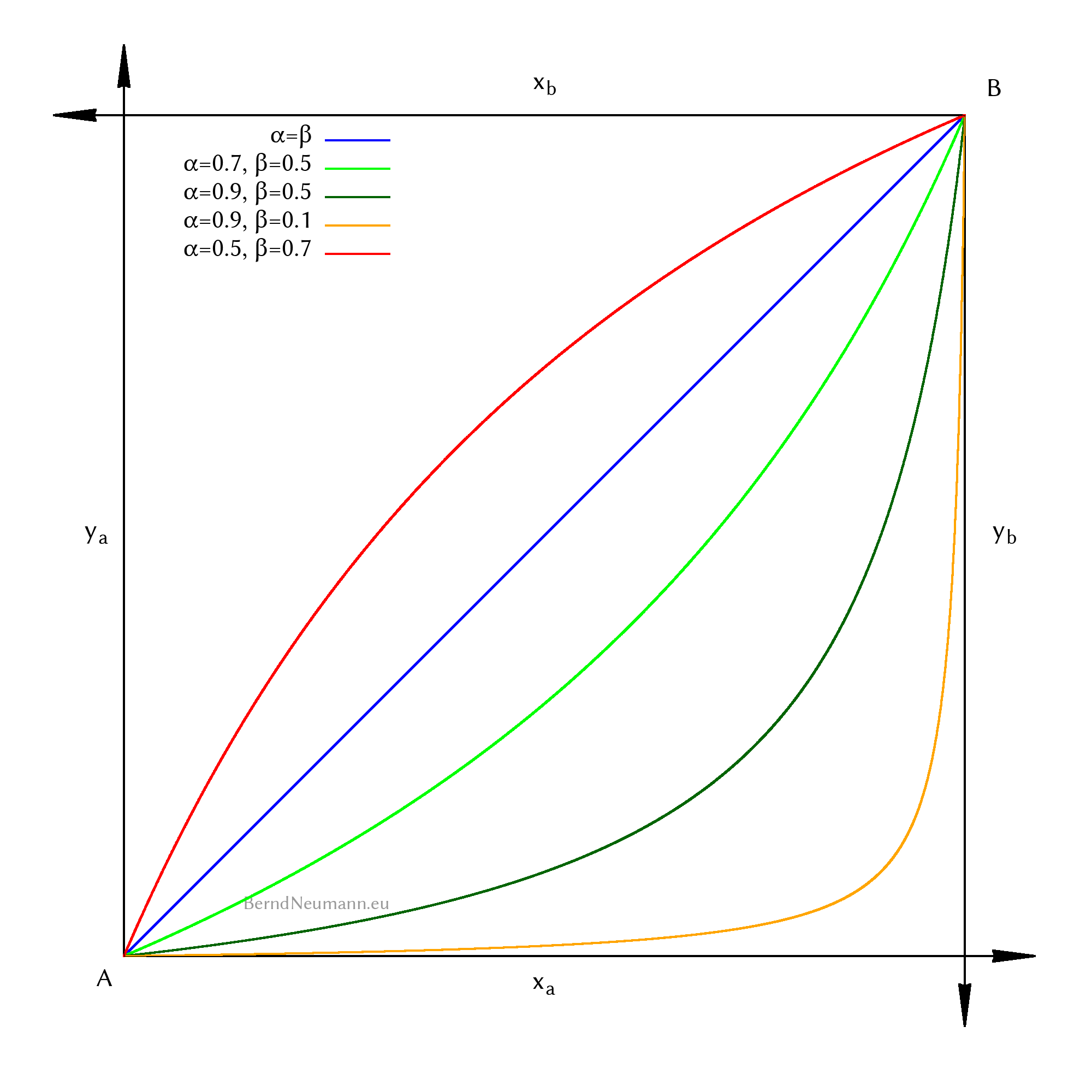
Die von der Kontraktkurve beschriebenen pareto-effizienten Allokationen sind wünschenswerte Zustände. Mit ihrer Herleitung aus den Nutzenfunktionen ist keinesfalls gezeigt, dass diese Zustände erreicht werden. Menschen handeln auf Märkten mit Gütermengen und Preisen, die bei der Herleitung der Kontraktkurve gar nicht vorkamen. Aus diesem Grund betonte ich weiter oben, dass die Konzepte der Pareto-Effizienz und des Marktgleichgewichts getrennt zu betrachten sind. Davon darf man sich nicht abbringen lassen, weil Tauschhandlungen in Richtung einer pareto-effizienten Allokation durch die linsenförmigen gemeinsamen Bessermengen offensichtlich sind und rational erscheinen. Man muß sich stets vor Augen halten, dass hier nicht zwei Individuen tauschen und der eine dem anderen ein Angebot zum gegenseitigen Vorteil macht. Es geht um Märkte, auf denen viele Individuen mit Gütermengen und Preisen handeln. So bleibt klar, dass wir mit der Herleitung der pareto-effizienten Allokationen über Wünschenswertes, nicht aber über das Resultat von Markthandlungen gesprochen haben.
5. Individuelle Nutzenmaximierung und Nachfragefunktionen
Nach der Analyse des Wünschenswerten drängt sich die Frage nach dem tatsächlichen Resultat des Handelns auf: Was passiert, wenn alle Individuen mit den Gütermengen und Preisen so umgehen, dass sie ihren persönlichen Nutzen maximieren? – Rechnen wir das für Person \(A\) analog zur Nutzenmaximierung in der partiellen Analyse aus. Die Nebenbedingung ist statt durch das Einkommen durch die mit den Preisen \(p_x\) und \(p_y\) bewertete Anfangsausstattung bestimmt: $$\begin{aligned} &\text{max}\;U_a(x_a, y_a)\\[1em] &NB: p_x x_a \; + \; p_y y_a \; \leq \; p_x \omega^x_a \; + \; p_y \omega^y_a \end{aligned}$$
Aufstellen der Lagrange-Funktion: $$ L(x_a, y_a, \lambda) \; = \; x_a^\alpha \, y_a^{(1-\alpha)} \, - \, \lambda \left( p_x \omega^x_a \; + \; p_y \omega^y_a \; - \; p_x x_a \; - \; p_y y_a \right) $$
Die partiellen Ableitungen werden gleich null gesetzt: $$\begin{aligned} \frac{\partial L}{\partial x_a} \; &= \; \alpha \; x_a^{(\alpha-1)} \; y_a^{(1-\alpha)} \; + \; \lambda p_x \; = \; 0\\[1em] \frac{\partial L}{\partial y_a} \; &= \; x_a^\alpha \; (1-\alpha) \; y_a^{-\alpha} \; + \; \lambda p_y = \; 0\\[1em] \frac{\partial L}{\partial \lambda} \; &= \; p_x x_a \; + \; p_y y_a \; - \; p_x \omega^x_a \; - \; p_y \omega^y_a \; = \; 0 \end{aligned}$$
Die Lösungen dieses Gleichungssystems sind die Marshall'schen Nachfragefunktionen. Um sie von anderen Gütermengen zu unterscheiden, markieren wir sie mit einem Stern. Er zeigt an, dass wir über eine Gütermenge nach Nutzenmaximierung sprechen: $$\begin{aligned} x_a^*(p_x, p_y) \; &= \; \frac{\alpha\;(p_x \omega^x_a \; + \; p_y \omega^y_a)}{p_x}\\[1em] y_a^*(p_x, p_y) \; &= \; \frac{(1-\alpha)\;(p_x \omega^x_a \; + \; p_y \omega^y_a)}{p_y}\\[1em] \end{aligned}$$
Analog dazu erhält man als Nachfragefunktionen für Individuum \(B\): $$\begin{aligned} x_b^*(p_x, p_y) \; &= \; \frac{\beta\;(p_x \omega^x_b \; + \; p_y \omega^y_b)}{p_x}\\[1em] y_b^*(p_x, p_y) \; &= \; \frac{(1-\beta)\;(p_x \omega^x_b \; + \; p_y \omega^y_b)}{p_y} \end{aligned}$$
In den Marshall'schen Nachfragefunktionen kommen drei Arten Variablen vor: Die Präferenzen in Form der Exponenten \(\alpha\) und \(\beta\), die Anfangsausstattungen und die Preise. Die ersten beiden stammen aus der Definition der Tauschökonomie (siehe oben) und sie sind das Mindeste, das als exogen gegeben vorausgesetzt werden muß. Daher behandeln wir sie als Konstanten. Die Preise hingegen kamen durch die Budgetrestriktion während der Nutzenmaximierung ins Spiel. Sie sind Variablen, und deswegen schreiben wir die Marshall'schen Nachfragefunktionen als eine Gütermenge in Abhängigkeit von den (variablen) Preisen. Wir sprechen über das nutzenmaximierende Handeln der Individuen am Markt, und die Frage ist: Zu welchen Preisen wird getauscht? – Bevor wir das ausrechnen, verweilen wir noch einen Moment bei den Nachfragefunktionen, da sich mit ihnen das Problem anschaulich skizzieren läßt. Diese Skizze wird erklären, warum wir die Analyse der Gütermärkte als eine Frage nach Preisen formulieren, und warum Preise die Antwort auf die Frage nach einem Allgemeinen Gleichgewicht sind.
Veranschaulicht haben wir die Marshall'schen Nachfragefunktionen in der partiellen Gleichgewichtsanalyse in einem Preis-Mengen-Diagramm. Das hilft in der allgemeinen Gleichgewichtsanalyse mit mehreren Gütern nicht weiter. Aber wir können die Marshall'schen Nachfragen für bestimmte Preise als Punkte in die Edgeworth-Box zeichnen, indem wir die entsprechenden Gütermengen \(x^*\) und \(y^*\) für diese Preise ausrechnen. Ein solcher Nachfrage-Punkt bedeutet, dass man von der Anfangsausstattung bei den entsprechenden Preisen zu diesem Güterbündel tauschen möchte und sich dieses Güterbündel zu diesen Preisen auch leisten kann. Man kann es sich so vorstellen: Wir sagen den Individuen Preise und dann zeigen beide auf das Güterbündel, das sie zu diesen Preisen gern hätten. Sie sind handelseinig, wenn beide auf die gleiche Allokation in der Edgeworth-Box zeigen.
Bevor wir diese Nachfragepunkte für verschiedene Preise in die Edgeworth-Box zeichnen, liegt es nahe, die Tauschkurve auszurechnen. Sie repräsentiert diese Nachfragepunkte für alle möglichen Preise. Dafür müssen wir für jede Person beide Nachfragefunktionen zusammenführen und die Preise eleminieren. Wir formen die Marshall'schen Nachfragefunktionen so um, dass die Preise als \(\frac{p_y}{p_x}\) auf einer Seite stehen. Für Person \(A\) erhalten wir dadurch: $$\begin{aligned} \frac{p_y}{p_x} \; &= \; \frac{x_a^* \; - \; \alpha \omega^x_a}{\alpha \omega^y_a}\\[1em] \frac{p_y}{p_x} \; &= \; \frac{(1-\alpha)\omega^x_a}{y_a^* \; - \; (1-\alpha) \omega^y_a} \end{aligned}$$
Durch Gleichsetzen und Umformen erhält man \(y_a^*(x_a^*)\): $$\begin{aligned} y_a^*(x_a^*) \; &= \; \frac{\alpha \omega^y_a(1-\alpha)\omega^x_a}{x_a^* \; - \; \alpha \omega^x_a} \; + \; (1-\alpha) \omega^y_a \end{aligned}$$
Für Person \(B\) ergibt sich analog \(y_b^*(x_b^*)\): $$\begin{aligned} y_b^*(x_b^*) \; &= \; \frac{\beta \omega^y_b(1-\beta)\omega^x_b}{x_b^* \; - \; \beta \omega^x_b} \; + \; (1-\beta) \omega^y_b \end{aligned}$$
Schauen wir uns in der Edgeworth-Box an, wie sich die Punkte der Marshall-Nachfrage bei verschiedenen Preisen über die Tauschkurve bewegen. Dabei ergeben sich für hohe Preise eines Gutes Randlösungen. Sie sind hier nicht weiter von Interesse.

Die Tauschkurven haben zwei Schnittpunkte. Einer liegt genau auf der Anfangsausstattung, weil es für beide Individuen Preise gibt, zu denen sie die Anfangsaustattung behalten möchten. Dies ist jedoch bei verschiedenen Preisen der Fall, so dass nur einer von beiden die Anfangsausstattung behalten möchte, während der andere Güter tauschen würde. Dieser Schnittpunkt hat keine weitere Bedeutung, weil die Individuen auf verschiedene Punkte in der Edgeworth-Box zeigen. Das ist bei dem anderen Schnittpunkt nicht der Fall. Wenn die Preisgerade genau durch ihn verläuft, liegen die Punkte der Marschall'schen Nachfrage beider Individuen genau übereinander, beide Individuen zeigen für diese Preise auf die gleiche Allokation der Edgeworth-Box. Nur in dieser Allokation und nur zu diesen Preisen haben wir Handschlag, Tausch und Allgemeines Gleichgewicht.
Die erwähnte Skizze (siehe oben) manifestiert sich in der Frage, wie wir diesen Schnittpunkt ausrechnen werden und wie wir sicherstellen, dass es ihn überhaupt gibt. Vielleicht hat sich der Schnittpunkt der Tauschkurven in der Grafik nur zufällig ergeben und existiert für andere Präferenzen und Anfangsausstattungen gar nicht. Um das herauszufinden, werden wir annehmen, dass die Marshall'schen Nachfragepunkte auf die gleiche Allokation der Edgeworth-Box zeigen, und dann die Preise suchen, die mit dieser Annahme konsistent sind. Finden wir Preise, die diese Annahme erfüllen, haben wir das Allgemeine Gleichgewicht; finden wir keine, verkürzte sich die Theorie des Allgemeinen Gleichgewichts auf die Feststellung, dass es keins gibt.
Mit dieser Skizze erscheint das Resultat des nutzenmaximierenden individuellen Handelns auf dem Markt offensichtlich, und die Lösung zum Greifen nah. Es lauert aber noch ein Fallstrick, den wir im nächsten Abschnitt aus dem Weg räumen werden, indem wir zuerst das Konzept der Überschußnachfrage
erläutern, um damit das Marktgleichgewicht zu definieren. Damit wenden wir uns dann dem erwähnten Fallstrick zu und erörtern die Relativität der Preise
im Zusammenhang mit dem Walras'schen Gesetz.
6. Walras'sches Gesetz, Überschußnachfrage und die Relativität der Preise
Im vorherigen Abschnitt haben wir die Marshall'schen Nachfragepunkte so beschrieben, dass wir Preise nennen und die Individuen auf das gewünschte Güterbündel zeigen. Von Interesse ist der Punkt, an dem beide auf die gleiche Allokation der Edgeworth-Box zeigen. Diesen Sachverhalt formulieren wir jetzt mathematisch, indem wir den Blick auf die angebotenen und nachgefragten Gütermengen richten: Ist die Marshall'sche Nachfrage größer als die Anfangsausstattung, möchte man von diesem Gut dazukaufen; ist sie kleiner, möchte man einen Teil seiner Anfangsausstattung verkaufen. Man nennt diese Differenz Überschußnachfrage (excess demand), und wir bezeichnen sie mit einem \(\Delta\): $$\begin{aligned} \Delta x_a^*(p_x, p_y) \; &= \; x_a^*(p_x, p_y) \; - \; \omega^x_a\\[1em] \Delta y_a^*(p_x, p_y) \; &= \; y_a^*(p_x, p_y) \; - \; \omega^y_a\\[1em] \Delta x_b^*(p_x, p_y) \; &= \; x_b^*(p_x, p_y) \; - \; \omega^x_b\\[1em] \Delta y_b^*(p_x, p_y) \; &= \; y_b^*(p_x, p_y) \; - \; \omega^y_b \end{aligned}$$
Die Gleichungen der Überschußnachfrage beschreiben, wie sich die Individuen am Markt verhalten. Mit ihnen können wir das Marktgleichgewicht für ein Gut definieren. Es liegt vor, wenn die angebotenen und nachgefragten Mengen für dieses Gut gleich sind, wenn also die Summe der Überschußnachfragen Null ist: $$\begin{aligned} \Delta x_a^* \; + \; \Delta x_b^* \; &= \; 0\\[1em] \Delta y_a^* \; + \; \Delta y_b^* \; &= \; 0 \end{aligned}$$
Diese Gleichungen bedeuten, dass die Marshall'schen Nachfragen beider Individuen auf die gleiche Allokation der Edgeworth-Box zeigen. Schreibt man die beiden Gleichungen für die Marktgleichgewichte statt mit Überschußnachfragen als Differenz zwischen Marshall'scher Nachfrage und Anfangsausstattung, sieht man, dass die Gleichungen für die Marktgleichgewichte den Feasibility-Bedingungen entsprechen. Marktgleichgewicht bedeutet also, dass die individuellen Konsumwünsche zu den entsprechenden Preisen konsistent zur Feasibility-Bedingung sind. In Abbildung 5 ist gut zu erkennen, dass die Marshall'schen Nachfragen keine Rücksicht darauf nehmen, ob dieser Konsumwunsch mit den Konsumwünschen der anderen Individuen vereinbar ist. Die drei Formulierungen, dass (1) die Marshall'schen Nachfragen auf die gleiche Allokation zeigen, dass (2) auf allen Gütermärkten die angebotene Menge gleich der nachgefragten Menge ist, und dass (3) die Marshall'schen Nachfragen konsistent zur Feasibility-Bedingung sind, beschreiben den gleichen Sachverhalt. Die Gleichungen für die Marktgleichgewichte drücken ihn mathematisch aus.
Angesichts der Gleichungen für die Marktgleichgewichte könnte man meinen, wir müßten nur noch die Überschuß- bzw. die Nachfragefunktionen einsetzen und könnten dann schauen, ob wir so die Preise erhalten, zu denen beide Gütermärkte im Gleichgewicht sind. Wir haben zwei Gleichungen und suchen zwei Preise. Die Lösung scheint trivial. Es steht aber noch der erwähnte Fallstrick im Weg. Für dessen Lösung sind das Konzept der Überschußnachfragen und die Definition des Marktgleichgewichts erforderlich.
Dafür schauen wir auf die Budgetrestriktion zurück. Sie enthält auf der einen Seite den Wert der Anfangsausstattung, also die mit den Preisen multiplizierten Gütermengen; und sie besagt, dass wir uns nur Güterbündel leisten können, deren Wert höchstens dem Wert der Anfangsausstattung entspricht. Das Güterbündel, das man sich gemäß seiner Marshall'schen Nachfrage leisten möchte, hat immer den gleichen Wert wie die Anfangsausstattung, denn niemand gibt sich damit zufrieden, bei einem Tausch weniger zu bekommen als er gegeben hat. In der geometrischen Anschauung sehen wir das daran, dass die Marshall'schen Nachfragepunkte mit Ausnahme der Randlösungen auf der Budgetgeraden liegen. Das gilt nicht nur für bestimmte Preise oder unter bestimmten Bedingungen, sondern das gilt per Definition der Marshall'schen Nachfragen als nutzenmaximales Güterbündel. Sein Wert ist daher dem Wert der Anfangsausstattung nicht nur gleich, sondern mit ihm identisch: $$\begin{aligned} p_x\,x_a^* \,+\, p_y\,y_a^* \; &\equiv \; p_x\,\omega^x_a \,+\, p_y\,\omega^y_a\\[1em] p_x\,x_b^* \,+\, p_y\,y_b^* \; &\equiv \; p_x\,\omega^x_b \,+\, p_y\,\omega^y_b \end{aligned}$$
Wir formen um, indem wir die Preise ausklammern und die Differenzen in den Klammern als Überschußnachfragen schreiben: $$\begin{aligned} p_x \, \Delta x_a^* \;+\; p_y \, \Delta y_a^* \; &\equiv \; 0\\[1em] p_x \, \Delta x_b^* \;+\; p_y \, \Delta y_b^* \; &\equiv \; 0 \end{aligned}$$
Diese beiden Identitäten besagen, dass der Wert der Summe der Überschußnachfragen jeder Person mit Null identisch ist. Daraus folgt, dass auch der über die Individuen aggregierte Wert der Überschußnachfragen mit Null identisch ist. Wir addieren die Gleichungen und klammern die Preise aus: $$\begin{aligned} p_x\,(\Delta x_a^* + \Delta x_b^*) \;+\;p_y\,(\Delta y_a^* + \Delta y_b^*) \; \equiv \; & 0 \end{aligned}$$
Diese Identität ist das Walras'sche Gesetz. – Schauen wir uns an, was daraus für die Gleichgewichtspreise folgt: In Walras' Gesetz stehen die aggregierten Überschußnachfragen jeweils eines Marktes, und wir hatten als Marktgleichgewicht definiert, dass diese Null sind. Angenommen der Markt für Gut \(X\) sei im Gleichgewicht, so dass $$\begin{aligned} \Delta x_a^* \; + \; \Delta x_b^* \; &= \; 0 \end{aligned}$$ gilt. Weiter wissen wir, dass die Preise \(p_x\) und \(p_y\) beide größer als Null sind. Aus dem Walras'schen Gesetz folgt dann, dass $$\begin{aligned} \Delta y_a^* \; + \; \Delta y_b^* \; &= \; 0 \end{aligned}$$ gelten muß. Ist also ein Gütermarkt im Gleichgewicht, folgt daraus, dass auch der andere Gütermarkt im Gleichgewicht ist. Bei einer Verallgemeinerung auf beliebig viele Güter wird man sehen, dass alle Gütermärkte im Gleichgewicht sind, wenn außer einem alle anderen im Gleichgewicht sind.
Damit offenbart sich, worin der Fallstrick besteht. Wir hatten oben die Marktgleichgewichte für beide (zwei) Gütermärkte formuliert und dachten intuitiv: Mit zwei Gleichungen bekommen wir für zwei (unbekannte) Preise eine eindeutige Lösung. Jetzt hat sich herausgestellt, dass eine der Gleichungen aus der anderen folgt. Wir haben daher nur eine Gleichung für zwei unbekannte Preise. Das sieht man in Abbildung 5 daran, dass es auf die Steigung der Budgetgeraden ankommt. Diese Steigung ist \(-\frac{p_y}{p_x}\). Wir suchen also ein Preisverhältnis, weil die Preise nur bis auf einen Preis bestimmt sind. Daher kann man den Preis eines Gutes als sogenanntes Numéraire gleich eins setzen und alle anderen Preise als relativen Preis bezogen auf dieses Gut verstehen. Für unseren Zwei-Güter-Fall werden wir den Bruch jedoch stehen lassen.
An dieser Stelle kommt die Darstellung der Tauschökonomie mit nur zwei Gütern an ihre Grenzen. Walras' Gesetz sagt, dass wir ein Gleichgewicht auf allen Gütermärkten haben, wenn wir ein Gleichgewicht auf allen außer einem Markt haben. In einer Ökonomie mit nur zwei Gütern ist alle außer einem
aber nur einer. Die schillernde Pointe des Allgemeinen Gleichgewichts, auf vielen interdependenten Märkten gleichzeitig ein Marktgleichgewicht zu haben, könnte dadurch verblassen. Diesen Umstand kann man sich mit dem Argument schön trinken, Gut \(X\) oder \(Y\) sei kein einzelnes Gut, sondern eine Kombination von Gütern. Dieses Argument ist zutreffend. Aber wie auch immer man es damit halten mag, ist wichtig zu wissen, dass das Prinzip auch bei zwei Gütermärkten das Gleiche ist, indem ein Gütermarkt stellvertretend für alle außer einem
steht, und beide Gütermärkte stellvertretend für viele (alle) Märkte
stehen.
7. Das Allgemeine Gleichgewicht
Wir wissen jetzt, dass wir in diesem Zwei-Güter-Fall die Gleichgewichtspreise bzw. ihren Quotienten erhalten, indem wir für nur einen Gütermarkt die Gleichgewichtsbedingung formulieren. Wir wählen Gut \(X\): $$\begin{aligned} \Delta x_a^* \; + \; \Delta x_b^* \; &= \; 0\\[1em] (x_a^* \;-\; \omega^x_a) \; + \; (x_b^* \; -\; \omega^x_b) \; &= \; 0 \end{aligned}$$
Wir setzen die Marshall'schen Nachfragefunktionen ein, die wir weiter oben ausgerechnet haben. Die Preise versehen wir mit einem Stern, um anzuzeigen, dass es sich um die Preise im Gleichgewicht handelt: $$\begin{aligned} \frac{\alpha\;(p_x^* \omega^x_a \; + \; p_y^* \omega^y_a)}{p_x^*} \;-\; \omega^x_a \; + \; \frac{\beta\;(p_x^* \omega^x_b \; + \; p_y^* \omega^y_b)}{p_x^*} \,-\,\omega^x_b\ \; &= \; 0 \end{aligned}$$
Diese Gleichung lösen wir zum Preisverhältnis auf und erhalten: $$\begin{aligned} \frac{p_y^*}{p_x^*} \; &= \; \frac{(1-\alpha)\omega^x_a+(1-\beta)\omega^x_b}{\alpha\omega^y_a + \beta\omega^y_b} \end{aligned}$$
In dieser Gleichung sind die Preise durch die Exponenten der Nutzenfunktionen und die Anfangsausstattungen bestimmt, also ausschließlich durch Variablen, die diese Tauschökonomie definieren. Wir erhalten Preise für alle möglichen Exponenten und Anfangsausstattungen, denn sowohl Zähler als auch Nenner der Gleichung sind immer eine positive Zahl. Es kann nicht vorkommen, dass die Preise nicht definiert wären, weil der Nenner null ergäbe.
Die Preise \(p_x^*\) und \(p_y^*\) beschreiben ein Gleichgewicht auf dem Markt für Gut \(X\), und das ist ein Gleichgewicht auf allen Gütermärkten außer einem. Nach dem Walras'schen Gesetz sind zu diesen Preisen also alle Gütermärkte im Gleichgewicht. Damit ist gezeigt, dass für alle gültigen Exponenten der Nutzenfunktionen und alle gültigen Anfangsausstattungen ein Allgemeines Gleichgewicht existiert: $$\begin{aligned} \Delta x_a^*(p_x^*, p_y^*) \; + \; \Delta x_b^*(p_x^*, p_y^*) \; &= \; 0\\[1em] \Delta y_a^*(p_x^*, p_y^*) \; + \; \Delta y_b^*(p_x^*, p_y^*) \; &= \; 0 \end{aligned}$$
Das Allgemeine Gleichgewicht nennt man auch Walras-Gleichgewicht oder kompetetives Gleichgewicht. Die beiden Gleichungen beschreiben es anhand der Überschußnachfragen mit Blick auf die Märkte für Gut \(X\) und Gut \(Y\). So beschreibt es auch Hal Varian (1987: S. 592). Eine interessante Alternative bietet Andreu Mas-Colell (1995: S. 519), indem er das Walras-Gleichgewicht aus Sicht der Individuen beschreibt. Dafür definiert er alle Güterbündel \((x_i^{'}; y_i^{'})\), die sich das Individuum \(i\) zu den Preisen \((p_x^*; p_y^*)\) leisten kann mit einer von den Preisen abhängigen Budgetmenge \(\mathbb{B}(p_x^*; p_y^*)\). Ein Walras-Gleichgewicht liegt dann vor, wenn alle Individuen das beste Güterbündel \((x_i^*; y_i^*)\) realisieren, das sie sich zu den Preisen \((p_x^*; p_y^*)\) leisten können: $$\begin{aligned} U(x_i^*; y_i^*) \geq U(x_i^{'}; y_i^{'}) \qquad \forall\;\;(x_i^{'}; y_i^{'})\in\mathbb{B}(p_x^*; p_y^*) \end{aligned}$$
Der beschriebene Sachverhalt ist der gleiche, nur dass in diesem Fall sowohl die Formulierung mit Worten als auch die Gleichungen verschieden sind. Dass beide Formulierungen äquivalent sind, kann man sich leicht klar machen: Wenn jeder das beste Güterbündel realisiert, das er sich zu diesen Preisen leisten kann, dann muß er es gegen seine Anfangsausstattung eintauschen können. Dafür muß er auf dem Markt für jedes Gut seine Überschußnachfrage tauschen können, es müssen also die Überschußnachfragen aller Individuen miteinander vereinbar sein, so dass die Summe aller Überschußnachfragen für jedes Gut null sein muß. – Da beide Formulierungen äquivalent sind, beschreiben sie die gleichen Preise. Durch die unterschiedlichen Formulierungen des Walras-Gleichgewichts wird klar, warum man sagt, ein Walras-Gleichgewicht sei eben dieser Preisvektor. Denn wesentlich für das Walras-Gleichgewicht sind die Preise, und nicht wie man die Definition im Detail formuliert.
Diesen Preisvektor haben wir in dieser Tauschökonomie für alle gültigen Nutzenfunktionen und Anfangsausstattungen ausgerechnet und so die Existenz des Allgemeinen Gleichgewichts gezeigt. Damit ist das Wesentliche gesagt. Der Vollständigkeit halber rechnen wir noch die Gütermengen im Gleichgewicht aus, indem wir die Gleichgewichtspreise in die Marshall'schen Nachfragefunktionen einsetzen. Diese Gütermengen markieren wir dafür mit einem zweiten Stern, um anzuzeigen, dass es sich um nutzenmaximale Gütermengen zu Gleichgewichtspreisen handelt: $$\begin{aligned} x_a^{**} \; &= \; x_a^*\,(p_x^*, p_y^*)\\[1em] y_a^{**} \; &= \; y_a^*\,(p_x^*, p_y^*) \end{aligned}$$
Die Preise verschwinden aus den Gleichungen und wir erhalten eine Gleichgewichtsallokation, die nur von Anfangsausstattungen und Präferenzen abhängt: $$\begin{aligned} x_a^{**} \; &= \; \alpha \omega^x_a \; + \; \frac{\alpha (1-\alpha)\omega^x_a\omega^y_a+\alpha (1-\beta)\omega^x_b\omega^y_a}{\alpha\omega^y_a + \beta\omega^y_b}\\[1em] y_a^{**} \; &= \; (1-\alpha)\omega^y_a \; + \; \frac{\alpha(1-\alpha)\omega^y_a\omega^x_a+(1-\alpha)\beta\omega^y_b\omega^x_a}{{(1-\alpha)\omega^x_a+(1-\beta)\omega^x_b}} \end{aligned}$$
Die entsprechenden Mengen für Person \(B\) kann man genauso ausrechnen. Man kann es sich aber auch einfach machen und dafür die Feasibility-Bedingung heranziehen: $$\begin{aligned} x_b^{**} \; &= \; \omega^x_a \,+\, \omega^x_b \,-\, x_a^{**}\\[1em] y_b^{**} \; &= \; \omega^y_a \,+\, \omega^y_b \,-\, y_a^{**} \end{aligned}$$
Dieses Gleichgewicht ist das Resultat des Marktgeschehens, das wir ganz zu Anfang (siehe oben) dem Wünschenswerten gegenübergestellt hatten. Alle Gleichungen hängen nur noch von den Präferenzen und Anfangsausstattungen ab. Die folgende Darstellung veranschaulicht, wie sich der Gleichgewichtspunkt bewegt, wenn sich Präferenzen oder Anfangsausstattung verändern:

8. Begründung des Marktgleichgewichts
Wir haben bei der Begründung des Allgemeinen Gleichgewichts eine Kleinigkeit außer Acht gelassen. Die Gleichgewichtspreise garantieren zwar, dass ein Allgemeines Gleichgewicht möglich ist, jedoch begründen sie nicht, dass es realisiert wird. Das Walras-Gleichgewicht fußt, wie alles in der Mikroökonomik, auf dem Begründungsschema der individuellen Nutzenmaximierung. Sie stand am Anfang der Berechnung (siehe oben) und ist in allen Gleichungen in Form der (nutzenmaximalen) Marshall'schen Nachfrage enthalten. In den Marshall'schen Nachfragefunktionen sind die Individuen Preisnehmer: Sie variieren die angebotenen und nachgefragten Gütermengen für gegebene Preise. Das ist ein Problem, wenn wir die Anpassung der Preise ebenfalls als individuelle Nutzenmaximierung erklären wollten. Denn wer sollte Änderungen an Preisen veranlassen, wenn alle Individuen sich als Preisnehmer verstehen (vgl. Varian 1978: Ch. 21.4, p. 398)? Wir haben ein Begründungsproblem.
Die Ursache dieses Begründungsproblems ist, dass die Theorie des Allgemeinen Gleichgewichts zur komparativen Statik gehört, während die Frage nach dem Tâtonnement-Prozeß, also dem Prozeß des Herantastens
an das Gleichgewicht, eine dynamische Analyse erfordert. Metaphorisch gesprochen haben wir das Zielphoto eines 10-Kilometer-Laufs und stellen fest, dass dieses Photo die berechtigte und sinnvolle Frage, wie das Rennen ablief, nicht beantworten kann. Es wird auf dieses Begründungsproblem daher keine elegante Gleichung geben, mit der es sich aus der Welt schaffen ließe. Die Frage ist, wie man damit umgeht, und die Antwort eine des persönlichen Geschmacks.
Andreu Mas-Colell trennt die statische Analyse strikt von der dynamischen. Zur Definition des Gleichgewichts auf einem Markt bemerkt er knapp: At a market equilibrium where consumers take prices as given, markets should clear.
(Mas-Colell 1995: Sec. 15.B, p. 518) Nur der Konjunktiv weist leise darauf hin, dass da ein Problem sein könnte. Die dynamische Analyse hat bei Mas-Colell in einem späteren Kapitel (Mas-Colell 1995: Sec 17.H, p. 620 ff) ihren Platz. Der Vorteil ist, dass man so vermeidet, an die statische Analyse Fragen der Dynamik heranzutragen, die diese gar nicht beantworten kann. Der Nachteil ist, dass man damit eine naheliegende Frage genauso strikt übergeht, wie man Statik und Dynamik getrennt hat.
Etwas mehr Begründung kann man implizit aus Walras' Wissenschaftsbegriff der Ökonomik herauslesen. Wissenschaft, so Walras, sei darauf angewiesen, von der Wirklichkeit zu abstrahieren (Walras 1874: Sec. 30, p. 27 f); und auf wirklichen Märkten sehen wir, dass diese von selbst zum Gleichgewicht neigen (Walras 1874: Sec. 61, p. 66 f). Damit hätte man eine empirische Begründung für die idealisierten Gleichungen der Marktgleichgewichte. Der Vorteil ist, dass man den Bezug zu echten Märkten anspricht. Der Nachteil ist, dass ein empirisches Argument theoretisch nicht überzeugen kann. Man beantwortet die Frage, warum der Stein zu Boden falle, nicht mit der Gravitation, sondern mit der Feststellung, dass er am Ende immer am Boden liege.
Hal Varian geht mit einem Walras'schen Auktionator den wohl populärsten Weg. Man solle sich vorstellen, auf allen Märkten rufe ein Auktionator Preise aus, woraufhin die Marktteilnehmer gemäß ihrer Marshall'schen Nachfragefunktionen die Gütermengen nennen, die sie zu diesen Preisen anbieten und nachfragen. Den Preis passe der Auktionator so lange an, bis das Angebot gleich der Nachfrage ist, und erst zu diesem Preis finde der Tausch tatsächlich statt. (vgl. Varian 1978: p. 398 und 1987: p. 588) Dabei ist sich Varian darüber im Klaren, dass Walras selbst es mit diesem Auktionator nie so gemeint hat. Walras deutet diese Idee zwar im Vorwort an (Walras 1874: Preface, p. ix), aber er denkt nicht an einen imaginären Auktionator, den man sich auf allen Märkten vorstellen müsse, sondern führt solche wohlorganisierten Märkte als anschauliches Beispiel für den Wettbewerb an (vgl. Walras 1874: Sec. 41, p. 42 f). Sehr treffend nennt Varian daher den Walras'schen Auktionator eine elaborate mythology
(Varian 1978: 398), die das Paradox lösen solle, dass Preisnehmer die Preise anpassen müssen.
Der Vorteil des Walras'schen Auktionators ist, eine kurze und anschauliche Erklärung der fraglichen Paradoxie zu liefern, in der die Individuen konsistent zu den Marshall'schen Nachfragefunktionen als Preisnehmer auftreten. Der gravierende Nachteil ist neben dem Umstand, Walras damit etwas unterzuschieben, was er so nie gesagt hat, dass wir über freie Märkte sprechen wollen und uns dafür einen imaginären Preis-Diktator vorstellen sollen, der das geforderte Marktgleichgewicht erzwingt.
Ich möchte einen anderen Weg vorschlagen. Der Ansatzpunkt ist, klar zu benennen, dass ein Modell der komparativen Statik den Prozeß zum Gleichgewicht nicht erklären kann. Möchte man ihn zumindest plausibel machen, ohne dafür ein neues Kapitel der Mikroökonomik aufzuschlagen, muß man den Begriff Preisnehmer
etwas freier auslegen, indem man sagt, dass ein Verkäufer zwar nicht teurer verkaufen könne als die anderen, wohl aber günstiger. Schauen wir auf den Verkäufer eines Gutes, dessen Preis höher ist als im Walras-Gleichgewicht. Er beginnt den Handel mit seiner Anfangsausstattung und tauscht Stück für Stück entlang der Preisgeraden in Richtung seines Marshall'schen Nachfragepunktes. Aber bevor er diesen erreicht, findet er keine Käufer mehr, die zu diesem hohen Preis kaufen möchten. Der Verkäufer kann nicht sein nutzenmaximales Güterbündel realisieren, so dass die Indifferenzkurve des realisierten Güterbündels die Preisgerade schneidet, statt sie nur zu berühren. Dadurch muss es eine Überschneidung von Bessermenge und Möglichkeitsmenge geben. Würde er jetzt den Preis geringfügig senken und dadurch mehr verkaufen, kann er ein Güterbündel in dieser Schnittmenge realisieren und sich damit besserstellen. Die Senkung der Preise ist also für diesen Verkäufer rational. Das Gleiche gilt für alle Verkäufer dieses Gutes bis der Preis auf den des Walras-Gleichgewichts gesunken ist.
Der wesentliche Vorteil dieser Erklärung ist, mit individueller Nutzenmaximierung zu begründen wie es Walras ursprünglich gedacht hatte (Walras 1874: Lesson 8, p. 77 ff), ohne dass man ein neues Kapitel der Mikroökonomik aufschlagen muß. Diesen großen Vorteilen stehen aber ebenso schwerwiegende Nachteile gegenüber: Die Umdeutung des Begriffs Preisnehmer
scheint geringfügig, ist aber mit dem Preisnehmer im Sinne Marshall'scher Nachfrager nicht vereinbar. Die Erklärung ist inkonsistent. Weiter suggeriert sie, ein mathematisches und somit wohlbegründetes Modell zu sein; ist aber eher eine plausible Kritzelei in den vorhandenen Diagrammen. Bei dieser Erklärung sind die Vorteile und Nachteile am größten. Nach gründlicher Abwägung meine ich, dass man mit dieser Erklärung unter dem Strich das kleinere Übel wählt.
Drei Aspekte sollten wir festhalten: 1. Die Theorie des Allgemeinen Gleichgewichts ist komparative Statik, und sie kann das Zustandekommen des per Definition vorausgesetzten Marktgleichgewichts nicht erklären. 2. Das Walras-Gleichgewicht ist trotzdem kein Luftschloß mathematischer Gleichgewichtsphantasien. Verschiedene heuristische Begründungen machen das Zustandekommen des Gleichgewichts plausibel. Keine davon ist makellos, aber für die Plausibilität sollte es reichen. Wer es genauer wissen möchte, muß sich zur dynamischen Gleichgewichtsanalyse des Tâtonnement-Prozesses verweisen lassen. 3. Die Frage nach dem Zustandekommen des Gleichgewichts führt uns lebhaft vor Augen, dass die Theorie des Allgemeinen Gleichgewichts auf den vollkommenen Wettbewerb vieler Individuen angewiesen ist. Diesen Aspekt werden wir im Exkurs über Edgeworth' Kritik noch einmal aufgreifen.
9. Der Erste Hauptsatz der Wohlfahrtsökonomik
Wir haben zuerst mit der Grenzrate der Substitution das Konzept der Pareto-Effizienz (siehe oben) erklärt, um zu zeigen, welche Allokationen in der Edgeworth-Box wünschenswert sind. Die Menge dieser Allokationen haben wir als Kontraktkurve (siehe oben) dargestellt. Anschließend haben wir ausgerechnet, welche Allokation realisiert wird, wenn die Individuen, jedes für sich und unter vollkommener Konkurrenz zueinander, ihren Nutzen maximieren (siehe oben). Dies ergab die Allokation des Allgemeinen Gleichgewichts (siehe oben). Jetzt werden wir untersuchen, welcher Zusammenhang zwischen der Allokation des Allgemeinen Gleichgewichts und den wünschenswerten pareto-effizienten Allokationen besteht.
Mit intuitiven Argumenten geht das ganz flink: Aus der partiellen Gleichgewichtsanalyse wissen wir, dass die Grenzrate der Substitution gleich dem Preisverhältnis ist, wenn ein Individuum sein Nutzenmaximum erreicht. Im Allgemeinen Gleichgewicht erreicht jedes Individuum sein Nutzenmaximum zu den herrschenden Gleichgewichtspreisen. Da diese Preise für alle die gleichen sind, muß auch die Grenzrate der Substitution aller Individuen gleich sein. Daher muß die Allokation des Allgemeinen Gleichgewichts, wie sie unter vollkommenem Wettbewerb zustande kommt, eine pareto-effiziente Allokation sein. Anders gesagt: Durch freie Märkte und vollkommenen Wettbewerb erreichen wir, zumindest hinsichtlich der Pareto-Effienz, immer eine wünschenswerte Allokation. Jedes Walras-Gleichgewicht ist pareto-effizient. Dies ist der Erste Hauptsatz der Wohlfahrtsökonomik.
Schauen wir uns das in der Sprache der Gleichungen an, indem wir für beide Individuen ausrechnen, welche Grenzrate der Substitution sie bei der Allokation des Allgemeinen Gleichgewichts haben: $$\begin{aligned} \text{GRS}_a^x\Big(x_a^{**}, y_a^{**}\Big) \; &= \; \text{GRS}_a^x\Big(x_a^*(p_x^*, p_y^*), y_a^*(p_x^*, p_y^*)\Big)\\[1em] \text{GRS}_b^x\Big(x_b^{**}, y_b^{**}\Big) \; &= \; \text{GRS}_b^x\Big(x_b^*(p_x^*, p_y^*), y_b^*(p_x^*, p_y^*)\Big) \end{aligned}$$
Auf der rechten Seite beider Gleichungen setzen wir die Funktion der Grenzrate der Substitution ein, wie wir sie weiter oben hergeleitet hatten: $$\begin{aligned} \text{GRS}_a^x\Big(x_a^{**}, y_a^{**}\Big) \; &= \; - \; \frac{\alpha}{1-\alpha} \; \frac{y_a^*(p_x^*, p_y^*)}{x_a^*(p_x^*, p_y^*)}\\[1em] \text{GRS}_b^x\Big(x_b^{**}, y_b^{**}\Big) \; &= \; - \; \frac{\beta}{1-\beta} \; \frac{y_b^*(p_x^*, p_y^*)}{x_b^*(p_x^*, p_y^*)} \end{aligned}$$
Wir setzen die Marschall'schen Nachfragefunktionen ein, die wir durch die Nutzenmaximierung der Individuen (siehe oben) hergeleitet hatten. $$\begin{aligned} \text{GRS}_a^x\Big(x_a^{**}, y_a^{**}\Big) \; &= \; - \; \frac{\alpha}{1-\alpha} \; \frac{\frac{(1-\alpha)\;(p_x^* \omega^x_a \; + \; p_y^* \omega^y_a)}{p_y^*}}{\frac{\alpha\;(p_x^* \omega^x_a \; + \; p_y^* \omega^y_a)}{p_x^*}} \\[1em] \text{GRS}_b^x\Big(x_b^{**}, y_b^{**}\Big) \; &= \; - \; \frac{\beta}{1-\beta} \; \frac{\frac{(1-\beta)\;(p_x^* \omega^x_b \; + \; p_y^* \omega^y_b)}{p_y^*}}{\frac{\beta\;(p_x^* \omega^x_b \; + \; p_y^* \omega^y_b)}{p_x^*}} \end{aligned}$$
Durch Kürzen erhält man, dass beide Grenzraten der Substitution gleich dem negativen Verhältnis der Gleichgewichtspreise sind: $$\begin{aligned} \text{GRS}_a^x\Big(x_a^{**}, y_a^{**}\Big) \; &= \; - \; \frac{p_x^*}{p_y^*} \\[1em] \text{GRS}_b^x\Big(x_b^{**}, y_b^{**}\Big) \; &= \; - \; \frac{p_x^*}{p_y^*} \end{aligned}$$
Also ist die Grenzrate der Substitution von Individuum \(A\) gleich der Grenzrate der Substitution von Individuum \(B\), und die Allokation des Allgemeinen Gleichgewichts mit den konsumierten Gütermengen \(x_a^{**}\), \(y_a^{**}\), \(x_b^{**}\), \(y_b^{**}\) eine pareto-effiziente Allokation. $$\begin{aligned} \text{GRS}_a^x\Big(x_a^{**}, y_a^{**}\Big) \; &= \; \text{GRS}_b^x\Big(x_b^{**}, y_b^{**}\Big) \end{aligned}$$
Zum Abschluß veranschaulicht das folgende Grafik diesen Zusammenhang in der Edgeworth-Box. Damit man aber in diesen Bildern die Überzeugungskraft mathematischer Klarheit im Sinne von Walras (1874: Lesson 3, Section 30) oder sogar eine Ästhetik der Méchanique Sociale
nach dem Vorbild der Méchanique Celeste
(Edgeworth 1881: 12) erkennen kann, sollte man sich daran erinnern, dass die pareto-effizienten Allokationen der Kontraktkurve auf ganz anderem Wege zustande kamen als das durch den dunkelgrünen Punkt dargestellte Walras-Gleichgewicht – und trotzdem liegt das Walras-Gleichgewicht für verschiedene Präferenzen und Anfangsausstattungen genau auf der Kontraktkurve.

10. Exkurs: Edgeworth und die Vollkommenheit der Märkte
Wir haben mit mathematischen Mitteln gezeigt, dass freie Märkte effizient sind. Dabei haben wir zwar mit einer Zwei-Güter-Zwei-Personen Tauschökonomie gerechnet und diese in der Edgeworth-Box veranschaulicht, haben aber eigentlich vollkommene Märkte mit vielen Marktteilnehmern gemeint. Hal Varian bietet die Erklärung an, die zwei Personen repräsentieren die durchschnittlichen Präferenzen von zwei unterschiedlichen Konsumenten-Typen (Varian 1987: 588), und Andreu Mas-Colell weist darauf hin, es gehe darum, das Prinzip auf möglichst einfache Art und Weise darzustellen (Mas-Colell 1995: 516, 526). Beides ist zutreffend, und es ist mathematisch keine Zauberkunst, die Darstellung auf beliebig viele Individuen und Güter zu erweitern. Das funktioniert aber nur algebraisch und man muß auf die Anschaulichkeit einer Edgeworth-Box verzichten.
Durch die Darstellung in der Edgeworh-Box sollte uns aber nicht entgehen, dass wir vollkommene Märkte vorausgesetzt haben und es ist wichtiger, diese Annahme kritisch zu reflektieren, als nur die Darstellung in der Edgeworth-Box zu rechtfertigen. Bei solcher Kritik muß es nicht notorisch darum gehen, die Annahme als falsch und die Mathematik der reinen Ökonomik als Hokuspokus hinstellen zu wollen. Ganz im Gegenteil: Die Mathematik ist ein scharfes Analyseinstrument, mit dem im Zuge der Neoklassik innerhalb erstaunlich kurzer Zeit eine ausgefeilte Theorie entwickelt wurde. Die Stärke der Mathematik liegt mitunter darin, eine Annahme wie die Vollkommenheit der Märkte präzise zu benennen und sie einer gezielten Kritik dadurch überhaupt erst zugänglich zu machen.
Marie-Esprit Léon Walras legte 1874 in den Éléments d'Économie Politique Pure ou Théorie de la Richesse Sociale
einen ersten Entwurf des mathematisch formulierten Allgemeinen Gleichgewichts vor, das Francis Ysidro Edgeworth schon wenige Jahre später in Mathematical Psychics
(1881) mit detaillierten mathematischen Erwägungen kritisiert. Seine Kritik richtet sich auf die Annahme perfekter Märkte, und er stellt vier strukturelle Imperfektionen vor. Dazu hier nur ein Beispiel: Der Arbeitsmarkt bestehe nicht aus vielen einzelnen Anbietern und Nachfragern von Arbeit, sondern aus einem Gewerkschaftsvertreter und einem Vertreter der Arbeitgeber, so dass sich dieser Markt trotz der großen Zahl involvierter Individuen verhält wie die Verhandlung zwischen nur zwei Parteien (vgl. Edgeworth 1881: 44f, 49).
Das geht weit über die lapidare Feststellung hinaus, die Wirklichkeit entspreche nie exakt dem idealisierten Modell, mit dem man sie erklärt. Edgeworth denkt an ein ganz anderes Modell. – Walras verglich die Annahme perfekter Märkte mit der Annahme reibungsfreier Kraftübertragung in der Mechanik (Walras 1874: Nr. 41); mit dieser Metapher begründet auch Varian (1978: 216). Der Gedanke ist, dass man die Funktionsweise von Märkten durch die vollkommene Konkurrenz in reiner Form
darstellt, und durch das mathematische Studium dieses Idealtyps das Wesen des Marktes erkennt, ohne die Theorie durch Reibungsverluste der Wirklichkeit unnötig kompliziert zu machen. Edgeworth hingegen meint, diese Idealisierung erfasse das Wesen des Marktes nicht hinreichend. Er zeichnet stattdessen das Bild eines Kontinuums, an dessen einem Ende der Fall des vollkommenen Wettbewerbs und am anderen Ende die Verhandlung zweier Personen steht. Eine Konsequenz davon ist, dass die mechanisch und wie ein law of Nature
anmutende eindeutige Bestimmtheit der Gleichgewichtsallokation, wie wir sie in Abbildung 7 und Abbildung 9 gesehen haben, wegfällt (Edgeworth 1881: Seite 46). Die Gleichgewichtsallokation ist je nach Ausmaß der Imperfektion eines Marktes nur noch mehr oder weniger bestimmt. Für den Fall der Verhandlung zwischen zwei Personen, kann man nur noch sagen, dass sie sich auf irgendeinen Punkt der Kontraktkurve innerhalb der gemeinsamen Bessermenge einigen werden (hier am besten in Abbildung 3b zu sehen). An die Stelle der Eindeutigkeit des Walras-Gleichgewichts tritt was heute als Edgeworth-Theorem bekannt ist: (\(\alpha\)) Contract without competition is indeterminate, (\(\beta\)) Contract with perfect competition is perfectly determinate, (\(\gamma\)) Contract with more or less perfect competition is less or more indeterminate.
(Edgeworth 1881: 20.)
Auf den ersten Blick scheint diese Kritik alles Bisherige in Frage zu stellen. Edgeworth kritisiert die Annahme, die das Modell von Anfang an und bis zum Ersten Hauptsatz der Wohlfahrtsökonomik stillschweigend begleitet. Er ist sich der Tragweite seiner Kritik wohl bewußt und deutet an einer Stelle über die Imperfektion durch Monopolstellungen an, nicht ohne furchtsam zu zögern, not without trembling
(Edgeworth 1881: Seite 47.), über Cournots Theorie des Monopols hinauszugehen. Das wiegt umso schwerer, da Edgeworth meint, Märkte werden mit der Zeit immer mehr zur Unvollkommenheit neigen (Edgeworth 1881: Seite 50). Aber auf eine Fundamentalkritik möchte Edgeworth nicht hinaus. Die Annahme vollkommener Konkurrenz hat mitsamt der zugehörigen Gleichgewichtsmathematik ihre Berechtigung, und über seine Kollegen William Stanley Jevons, Alfred Marshall und Léon Walras läßt Edgeworth nur lobende Worte fallen.
Edgeworth' Pointe ist eine andere: Das Walras-Gleichgewicht, wie wir es weiter oben hergeleitet haben, ist eindeutig durch die Präferenzen und die Anfangsausstattung bestimmt, und Walras meinte, der Preis im Gleichgewicht drücke den wahren Wert der Waren aus. Dieser Wert sei ein natural fact
(Walras 1874: Section 28) und das Gleichgewicht habe den Charakter eines vom menschlichen Willen unabhängigen Naturgesetzes. Der Wert unterliege nicht der menschlichen Entscheidungshoheit (Walras 1881: Section 23-26), so dass die Allokation des Gleichgewichts, also die abschließende Verteilung der Güter, keine ethische Frage sei. Edgeworth wendet sich gegen diese Trennung von Ökonomik und Ethik. Für seine Argumentation entwickelt er als Erster das Konzept der Kontraktkurve, und für ihn ist auch ohne den ersten Hauptsatz der Wohlfahrtsökonomik klar, dass rationale Individuen immer eine Allokation der Kontraktkurve innerhalb der gemeinsamen Bessermenge erreichen, weil beide Parteien daran ein Interesse haben (Edgeworth 1881: 29, 54). Aber die Interessen der Parteien stehen sich unvereinbar in der Frage gegenüber, welche Allokation der Kontraktkurve sie realisieren, denn dort ist jeder Gewinn des einen der Verlust des anderen. Dieser Gegensatz der Interessen sei das charakteristische Übel unvollkommener Märkte, und darum ging es Edgeworth mit dem Konzept der Kontraktkurve. Der Gegensatz führe zu Stillstand (»deadlock«) und motiviere zu Heuchelei und der anrüchigen Kunst des Feilschens (»objectionable arts of higgling«) (Edgeworth 1881: 29f).
Auflösen, so Edgeworth, könne diesen Gegensatz der Interessen nur ein ethisches Prinzip der Schlichtung (Edgeworth 1881: 51), so dass die Idee des Wettbewerbs um ethische Erwägungen ergänzt werden müsse. Der Trennung zwischen naturwissenschaftlich und mechanisch verstandener Ökonomik und Ethik setzt Edgeworth entgegen, dass ökonomisches Denken zwangsläufig zum ethischen Denken führt (Edgeworth 1881: 56). Dies ist die erstaunliche Schlußfolgerung, die Edgeworth aus der Kritik der angenommenen Vollkommenheit der Märkte ableitet. Wir sollten sie im Auge behalten, wenn wir heute über Kontraktkurve, Walras-Gleichgewicht und den Ersten Hauptsatz der Wohlfahrtsökonomik sprechen.
11. Abschließende Bemerkungen
Das Ziel dieses Artikels ist, in einer Tauschökonomie die Grundzüge der Theorie des Allgemeinen Gleichgewichts bis zum Ersten Hauptsatz der Wohlfahrtsökonomik so darzustellen, dass die Mathematik nicht nur geometrisch anschaulich, sondern in ihrer ökonomischen Bedeutung einleuchtend ist und die mathematische Art des ökonomischen Denkens greifbar wird, so dass manche Studentinnen und Studenten der Wirtschaftswissenschaften nach diesem Tutorial
nicht nur eine Klausuraufgabe lösen, sondern das Modell der Tauschökonomie selbstständig anwenden können. Sollte das gelungen sein, sind meine mit diesem Artikel verbundenen Erwartungen vollkommen erfüllt.
Darüber hinaus wäre ich froh, wenn im letzten Teil deutlich wurde, dass die kritische Auseinandersetzung mit der Ökonomik eine spannende Sache ist. Auch wenn man sich in den Wirtschaftswissenschaften mit kritischen Reflexionen schwerer tut als anderswo, mag durch Edgeworth spürbar geworden sein, dass solche Reflexionen das ökonomische Verständnis erweitern können und keinesfalls Blaupausen für Propagandasitzungen des Politbüros sein müssen.
Mit dem kritischen Ausflug zu Edgeworth ist auch die Hoffnung verbunden, in manchem Leser die Neugier auf die Texte der Klassiker angestachelt zu haben. Zwar ist das wirtschaftswissenschaftliche Studium größtenteils ein Lehrbuchstudium des state of the art
, die Lektüre der Klassiker bietet aber mehr als die Puzzelstücke, die Eingang in den Kanon der Lehrbücher gefunden haben. Das gilt, wie wir bei Edgeworth eindrucksvoll sehen konnten, besonders für die Frage nach dem Verhältnis von Ökonomie und Ethik. In Zeiten des Klimawandels und vermehrter Wirtschaftskrisen sollten Ökonomen mehr zu sagen haben als eine Internalisierung externer Effekte zu empfehlen. Klug ist daher der Rat, den Jevons (1871) am Ende seines Einführungskapitals gibt: Wir können Ökonomie abseits von moralischen Erwägungen studieren, aber wenn die Zeit es zuläßt, verbietet uns niemand, neben der wertfreien Ökonomik in Form ethischer Studien einen zweiten Grashalm wachsen zu lassen.
Literatur
Edgeworth, Fancis Ysidro (1881): Mathematical Psychics. An Essay on the Application of Mathematics to the Moral Sciences. London. Online in the McMaster University Archive for the History of Economic Thought.
Jevons, William Stanley (1871): The Theory of Political Economy. 5th Edition, New York 1965.
Mas-Colell, Andreu; Whinston, Michael D.; Green, Jerry R. (1995): Microeconomic Theory. New York, Oxford.
Varian, Hal Ronald (1987): Intermediate Microeconomics. A Modern Approach. 8th Edition, 2010. New York, London.
Varian, Hal Ronald (1978): Microeconomic Analysis. 3rd Edition 1992. New York, London.
Walras, Marie-Esprit-Léon (1874): Elements of Theoretical Economics or the Theory of Social Wealth. Translation of the 3rd Edition (1896) by Donald A. Walker and Jan van Daal. Cambridge University Press 2014.
Bernd Neumann,