Inhalt

1. Die Rationalität des Individuums

2. Die Indifferenzkurve

3. Die Nutzenfunktion

4. Die Budgetrestriktion

5. Die Nutzenmaximierung

6. Das Lagrange-Verfahren

7. Die Edgeworth-Box

8. Schlußbemerkung

1. Die Rationalität des Individuums

Die Mikroökonomik erklärt die Wirtschaft aus Sicht des einzelnen Individuums, folgt also dem Paradigma des Methodologischen Individualismus (Wikipedia: Methodologischer Individualismus). Die erste damit verbundene Annahme lautet, dass Individuen rational handeln. In der Terminologie der Ökonomie gesprochen maximieren sie ihren Nutzen, was so viel bedeutet wie ein möglichst großes Glück oder Wohlbefinden anzustreben. Man spricht oft vom Menschenbild des egoistischen Nutzenmaximierers. Das ist aber irreführend, denn es suggeriert, die Ökonomie erkläre die moralisch fragwürdige Eigenschaft des Egoismus zu ihrem anthropologischen Leitbild, den Egoismus gar zu einer moralisch wünschenswerten oder zumindest einer moralisch legitimen Eigenschaft. Das ist unzutreffend, denn Mikroökonomik ist ein Modell menschlichen Handelns in der Sphäre der Wirtschaft, und dieses Modell beansprucht nichts weiter als Wirtschaft zu erklären. Eine ethische Theorie oder philosophische Anthropologie ist damit nicht behauptet. Man kann es sich so vorstellen: Lädt jemand aufgrund seiner geselligen und freigiebigen Natur seine Freunde zum Grillen ein, dann wird er nicht zu einem moralisch fragwürdigen Egoisten, weil er etwas Geld sparen möchte und daher den Kasten Bier und die Grillkohle in dem Supermarkt kauft, der beides gerade im Sonderangebot hat. – Unberührt von diesem manchmal mißverstandenen Menschenbild bleibt, dass Ökonomie auch mit ethischen Fragen zu tun hat. In einem Exkurs des Tauschökonomie-Artikels (Exkurs: Edgeworth und die Vollkommenheit der Märkte) werde ich darauf zurück­kommen.

Die nutzenmaximierende Rationalität kocht auf einer anderen Flamme als eine ethische oder anthropologische Theorie: Mag jemand lieber Schokoladeneis als Vanilleeis, und wir bieten ihm an, entweder eine Kugel Schoko oder eine Kugel Vanille zu wählen, dann bedeutet nutzenmaximierende Rationalität, dass er mit der Kugel Schokoladeneis die Option wählt, die ihm lieber ist. Irrational wäre, die weniger günstige Option zu wählen, obwohl er sich hätte besser entscheiden können.

Im Modell der Mikroökonomik betrachten wir die Wahl zwischen Güterbündeln. Das ist die Kombination von mindestens zwei Gütern, die jeweils in einer bestimmten Menge darin enthalten sind. Dabei beschränken wir uns in der Regel auf zwei Güter, weil man den zweidimensionalen Fall mit Zeichungen gut veranschaulichen kann. Man schreibt ein Güterbündel üblicherweise als Tupel, indem man die enthaltenen Gütermengen in runde Klammern schreibt. Bei der Wahl zwischen den zwei Kugeln Eis wurde also das Güterbündel aus einer Kugel Schoko und null Kugeln Vanille \((1; 0)\) dem Bündel aus null Kugeln Schoko und einer Kugel Vanille \((0; 1)\) vorgezogen. Bietet man demjenigen eine Kugel Schoko \((1; 0)\) oder zwei Kugeln Vanille \((0; 2)\) an, dann könnte Vanille das Bündel seiner Wahl sein. Daran ist nichts Irrationales, denn wir betrachten nicht die Entscheidung zwischen Schoko und Vanille, sondern die Entscheidung zwischen Güterbündeln.

Die nutzenmaximale Entscheidung für ein bestimmtes Güterbündel setzt sich aus zwei Teilen zusammen: Zum einen beschreiben wir anhand der Präferenzen in Form einer Nutzenfunktion für jedes denkbare Güterbündel, welche anderen Güterbündel man besser, welche man schlechter und welche man gleich gut findet. Zum anderen beschreiben wir anhand der Budgetrestriktion, welche Güterbündel erreichbar sind, weil man sie sich leisten kann. Dies sind die Güterbündel der Budgetmenge oder Möglichkeitsmenge. Nutzenmaximierung bedeutet beide Teile zusammenzuführen, indem man ausrechnet, welches Güterbündel der Möglichkeitsmenge allen anderen darin enthaltenen Bündeln bevorzugt und somit als nutzenmaximales Güterbündel gewählt wird. An dieser Unterteilung orientiert sich die Gliederung der folgenden Abschnitte. Wir beginnen mit den Präferenzen.

2. Die Indifferenzkurve

Ich erwähnte, dass man sich in der Regel auf zwei Güter beschränkt, weil das hinreicht, um das Prinzip zu erklären und man den Zwei-Güter-Fall in Diagrammen veranschaulichen kann. Wir werden das auch so machen und nennen die Güter \(X\) und \(Y\). Die Menge, die man von Gut \(X\) hat, bezeichnen wir mit \(x\), die Menge an Gut \(Y\) mit \(y\), und ein Güterbündel schreiben wir dementsprechend als \((x; y)\). Zeichnen wir uns ein Gütermengendiagramm, in dem wir auf einer Achse die Gütermenge \(x\) und auf der anderen Achse die Gütermenge \(y\) auftragen. Die Punkte dieses Diagramms repräsentieren jedes erdenkliche Güterbündel.

In dieses Diagramm zeichnen wir ein Güterbündel \((x^{i}; y^{i})\) ein und fragen: Wie bewertet der Konsument dieses Güterbündel hinsichtlich des Nutzens im Vergleich zu anderen Güterbündeln? Welche Güterbündel zieht der Konsument dem Bündel \((x^{i}; y^{i})\) vor, welche findet er schlechter und welche genauso gut? – Die Annahme der Nichtsättigung besagt, dass ein Güterbündel immer vorgezogen wird, wenn es von mindestens einem Gut mehr enthält und von keinem Gut weniger. In Abbildung 1 sind das alle Bündel, die rechts über \((x^{i}; y^{i})\) liegen. Entsprechend findet der Konsument alle Güterbündel, die links unter \((x^{i}; y^{i})\) liegen, schlechter. Die Güterbündel, die man genauso gut findet wie \((x^{i}; y^{i})\), müssen auf einer Kurve liegen, die von \((x^{i}; y^{i})\) aus nach links oben und nach rechts unten verläuft. Diese Kurve aus Güterbündeln gleichen Nutzenniveaus heißt Indifferenzkurve. Dem Individuum ist egal, welches dieser Güterbündel es hat, denn die damit verbundene Wohlfahrt ist gleich. Alle Güterbündel, die oberhalb einer Indifferenzkurve liegen, werden den Güterbündeln der Indifferenzkurve vorgezogen. Sie bilden die Bessermenge (better set) für alle Bündel dieser Indifferenzkurve.

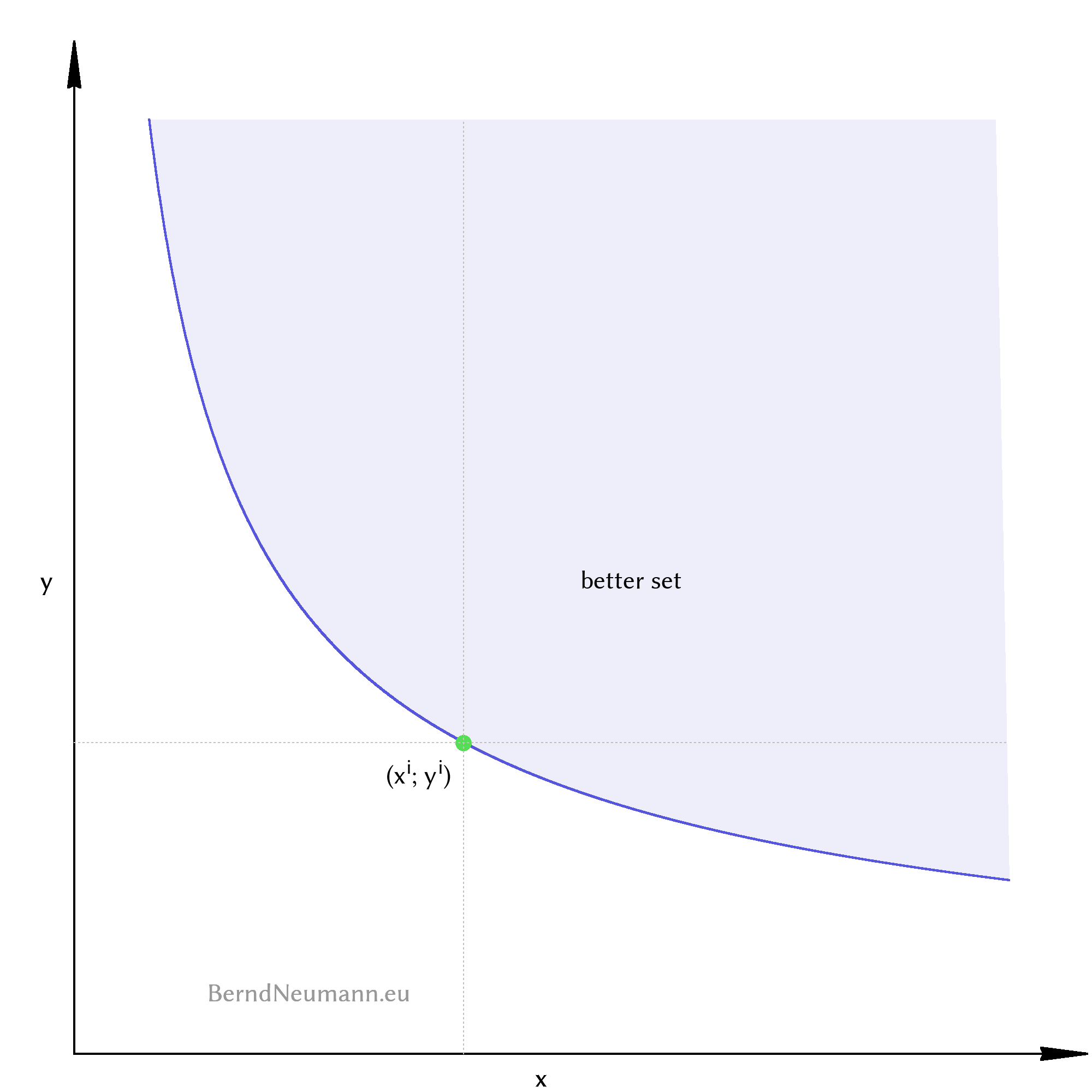
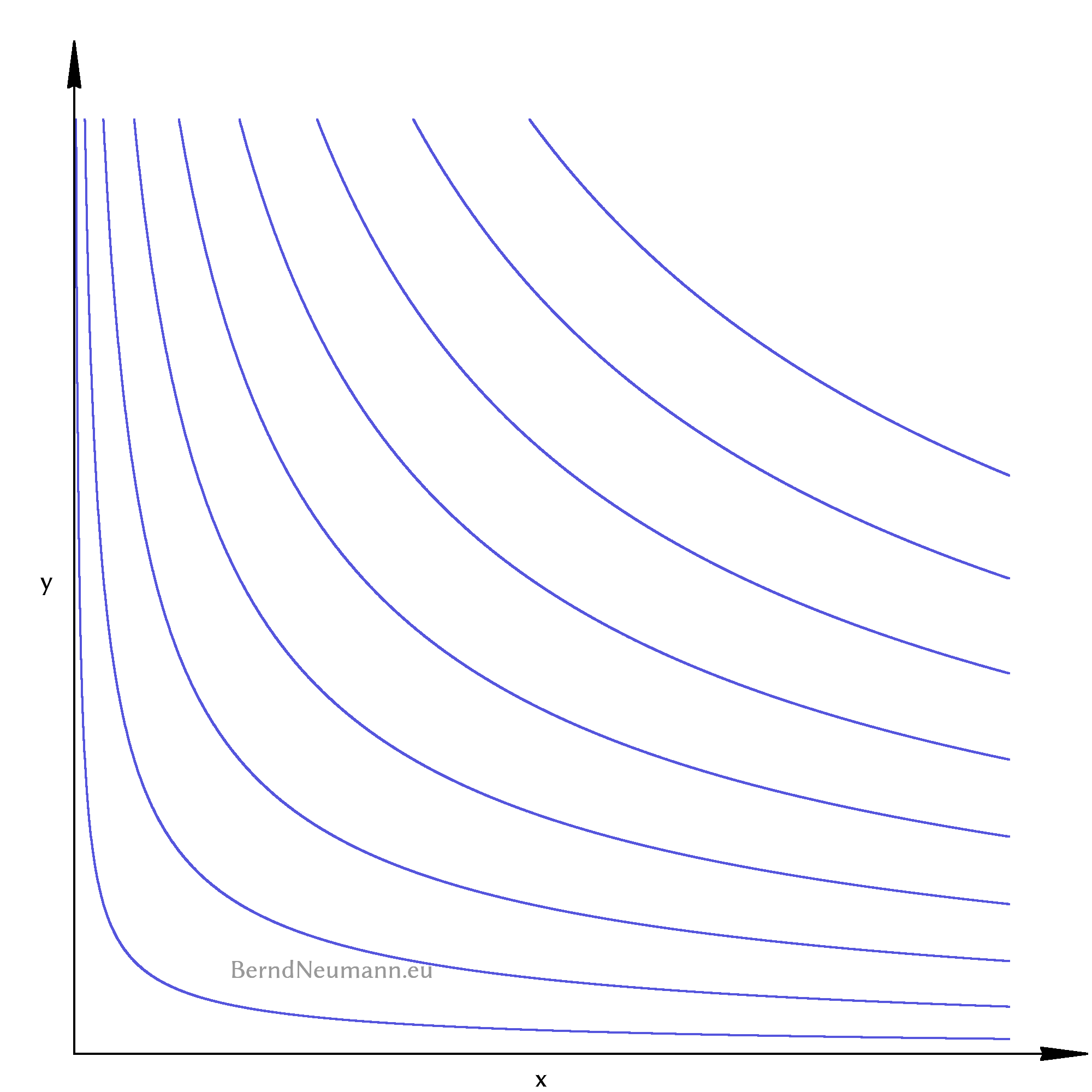
Indifferenzkurven können sich nicht schneiden. Würden sich Indifferenzkurven schneiden, dann wären die Güterbündel der einen Indifferenzkurve zum Teil besser, an einer Stelle gleich gut und zum Teil schlechter als die Bündel der anderen Indifferenzkurve. Das wäre irrational. Es gibt unendlich viele Indifferenzkurven, die unendlich nah beieinander liegen, aber sie schneiden sich niemals. Zeichnen wir uns ein paar Indifferenzkurven auf, um eine Anschauung davon zu gewinnen.

3. Die Nutzenfunktion

Unser Ziel ist es, für zwei beliebige Güterbündel sagen zu können, welches der Konsument besser findet oder dass er beide gleich gut findet. Abbildung 2 bringt uns dem näher, indem wir alle Indifferenzkurven von links unten nach rechts oben mit einer stetig steigenden Zahl durchnummerieren. Können wir dann über zwei Güterbündel sagen, welche Nummern ihre jeweiligen Indifferenzkurven haben, ist klar, welches vorgezogen wird. Diese Nummerierung leistet eine Nutzenfunktion, indem sie jedes Güterbündel mit einer Zahl versieht. Güterbündel mit der gleichen Zahl liegen auf der gleichen Indifferenzkurve, Güterbündel mit einer höheren Zahl liegen auf einer höheren, weiter rechts oben liegenden, Indifferenzkurve.

Für diese Durchnummerierung versieht man die Gütermengen mit einem Exponenten und multipliziert sie miteinander. Die Exponenten drücken aus, wie wichtig dem Individuum dieses Gut ist. Größere Exponenten zeigen eine stärkere Präferenz für dieses Gut an. Den Exponenten zur Menge an Gut \(X\) nennen wir \(\alpha_x\), den zur Menge an Gut \(Y\) entsprechend \(\alpha_y\). Beide Exponenten müsssen größer oder gleich null sein. Eine Nutzenfunktion bezeichnet man üblicherweise mit \(U\) vom Wort utility. Sie sieht grundsätzlich und im eingeschränkten Rahmen dieses Artikels wie folgt aus: $$\begin{aligned} U(x, y) \; &= \; x^{\alpha_x} \, y^{\alpha_y} \end{aligned}$$

Unter Nutzen, so hatte ich in den einleitenden Worten angedeutet, könne man sich so etwas wie Wohlbefinden oder Glück vorstellen. Das stimmt soweit Güterbündel mit einem höheren Wert der Nutzenfunktion zu mehr Wohlbefinden führen. Nutzen ist aber kein Maß für Wohlbefinden, sondern nur eine Durchnummerierung der Indifferenzkurven; ähnlich den Hausnummern einer Straße, die nicht messen, wie weit Häuser voneinander entfernt stehen, sondern nur die Reihenfolge der Häuser wiedergeben. Genauso bedeutet ein Nutzenwert von acht nicht doppelt so viel Wohlbefinden wie ein Nutzenwert von vier, sondern nur, dass der Konsument das Bündel mit dem höheren Nutzenwert vorzieht. Man spricht von einem ordinalen Nutzenbegriff, weil der Nutzenwert eine Ordinalzahl (Wikipedia: Ordinalzahl) ist. Auf diese Weise beschreibt eine Nutzenfunktion die Präferenzordnung oder die Präferenzen des Individuums. Da die Zahl des Nutzenwertes keine weitere Bedeutung hat, kann die gleiche Präferenzordnung durch unterschiedliche Nutzenfunktionen dargestellt werden. Diese geben den Indifferenzkurven zwar verschiedene Hausnummern, aber an ihrer Form und Reihenfolge ändert sich nichts. Man kann eine Nutzenfunktion quadrieren (beide Exponenten verdoppeln) oder die Wurzel ziehen (beide Exponenten halbieren) ohne dass sich etwas an den dargestellten Präferenzen ändert: Alle Güterbündel, die vorher den Nutzen zwei hatten, bekommen nach dem Quadrieren den Nutzenwert vier, und jene, die voher drei hatten, bekommen den Wert neun.

Diese Eigenschaft von Nutzenfunktionen verwenden wir, um die Nutzenfunktion so umzuschreiben, dass sich die Exponenten zu eins addieren. Eine solche Nutzenfunktion heißt Cobb-Douglas-Nutzenfunktion. Bei zwei Gütern können wir dadurch auf die Unterscheidung zwischen \(\alpha_x\) und \(\alpha_y\) verzichten und die Nutzenfunktion mit einem \(\alpha \in [0; 1]\) schreiben. Je größer \(\alpha\) ist, desto stärker die Vorliebe des Konsumenten für Gut \(X\). Die Cobb-Douglas-Nutzenfunktion lautet: $$\begin{aligned} U(x, y) \; &= \; x^{\alpha} \, y^{1-\alpha} \end{aligned}$$

Diese Nutzenfunktion ist dreidimensional. Sie ordnet jedem Punkt im zweidimensionalen Gütermengendiagramm in der dritten Dimension einen Nutzenwert zu. Es ergibt sich ein Nutzengebirge, das nach rechts und nach oben stetig ansteigt. – Da die Nutzenwerte unwichtig sind und nur ein größer oder kleiner wichtig ist, benötigen wir nur die Höhenlinien (Indifferenzkurven). Diese können wir zweidimensional einzeichnen und müssen nur wissen, dass eine Indifferenzkurve weiter rechts oben Güterbündel mit einem höheren Nutzenniveau repräsentiert.

Unterschiedliche Präferenzen stellen wir durch verschiedene Werte für \(\alpha\) dar. Wir werden später sehen, dass es vor allem darauf ankommt, wie flach oder steil die Indifferenzkurve durch ein Güterbündel verläuft. Die Steigung einer Indifferenzkurve in einem bestimmten Güterbündel ist die Grenzrate der Substitution. Sie gibt an, wie viel man von Gut \(Y\) gegen eine marginale Einheit von Gut \(X\) tauschen würde. Der Artikel zur Tauschökonomie wird sich damit ausführlich auseinandersetzen. – Schauen wir uns zum Abschluß dieses Teils über Nutzenfunktionen in bewegten Bildern die Form der Indifferenzkurven für verschiedene Werte von \(\alpha\) an:

4. Die Budgetrestriktion

Welche Güterbündel sich ein Individuum leisten kann, hängt davon ab, wie teuer die Güter sind und welche Mittel dem Individuum zur Verfügung stehen. Den Preis von Gut \(X\) nennen wir \(p_x\), den von Gut \(Y\) nennen wir \(p_y\). Das Produkt \(p_x x\) ist demnach, was das Individuum für Gut \(X\) ausgibt und \(p_y y\), was es für Gut \(Y\) ausgibt. Die Summe von beiden darf höchstens so groß sein wie das Einkommen des Individuums. Mit Blick auf die Tauschökonomie werden wir jedoch nicht von einem Einkommen sprechen, sondern annehmen, das Individuum verfüge über ein Güterbündel als Anfangsausstattung, die wir mit \((\omega^x; \omega^y)\) bezeichnen. Diese Anfangsausstattung, oder Teile davon, kann das Individuum jederzeit zu den geltenden Preisen \(p_x\) und \(p_y\) verkaufen, um von dem Erlös ein anderes Güterbündel zu kaufen. Die Budgetrestriktion oder Budgetbeschränkung lautet: Der Wert des konsumierten Güterbündels kann höchstens so groß wie der Wert der Anfangsausstattung (Einkommen) sein: $$\begin{aligned} p_x\;x \;+\; p_y\;y \;\;\;\; &\leq \;\;\;\; p_x\;\omega^x \;+\; p_y\;\omega^y \end{aligned}$$

Erfüllt ein Güterbündel \((x; y)\) die Budgetbeschränkung, ist es Teil der Budget- oder Möglichkeitsmenge. Wir formen die Ungleichung nach \(y\) um, damit wir sie in das Gütermengendiagramm einzeichnen können: $$\begin{aligned} y \; &\leq \; -\frac{p_x}{p_y}\,x \; + \; \frac{p_x\,\omega^x \; p_y\,\omega^y}{p_y} \end{aligned}$$

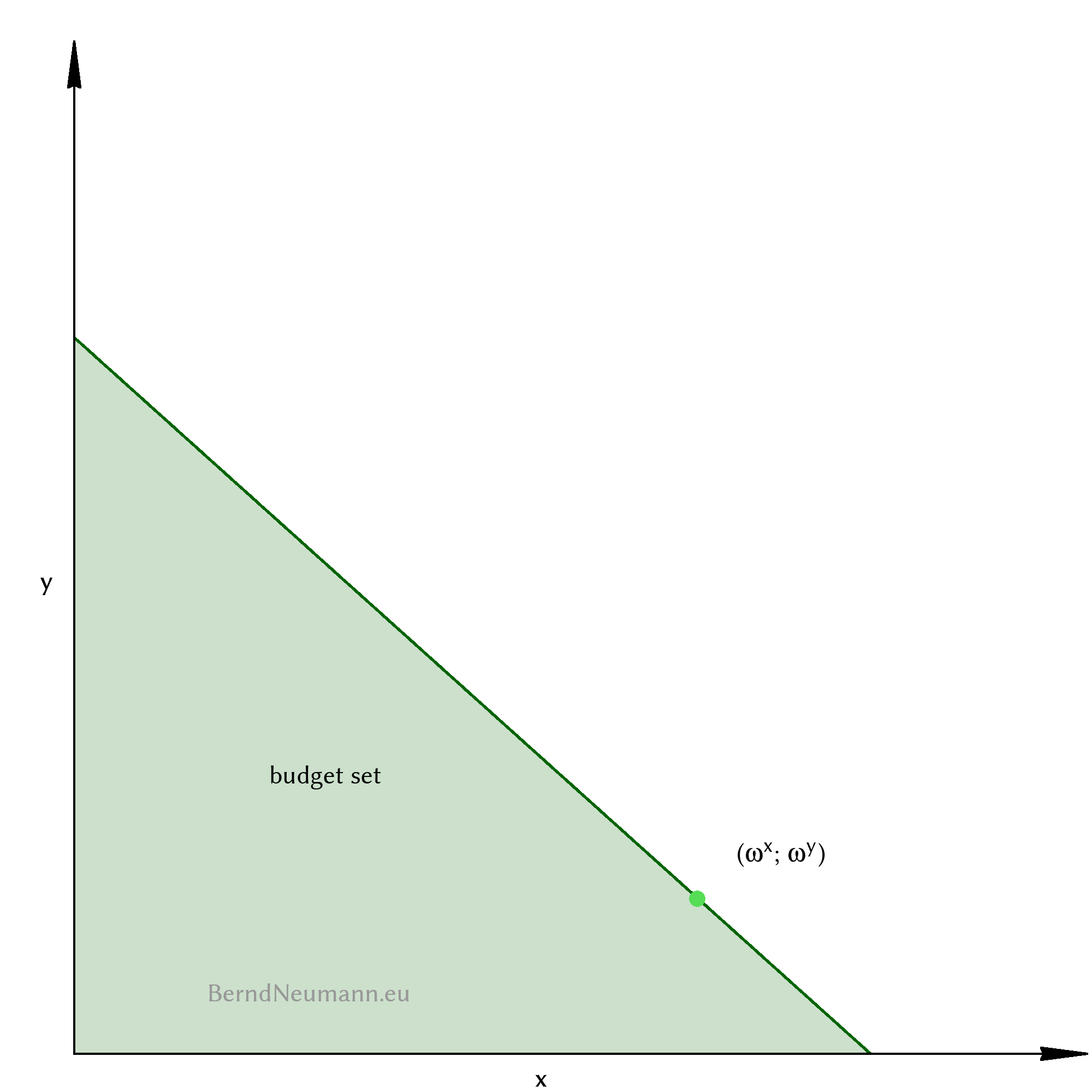
Die obere Grenze der Budgetmenge ist die Budgetgerade, die man in einer Tauschökonomie auch Preisgerade nennt. Man erhält ihre Gleichung, indem man das Kleinergleichzeichen durch ein Gleichheitszeichen ersetzt. Sie hat die Steigung \(-\frac{p_x}{p_y}\). Die \(y\)-Achse schneidet sie an der Stelle \(\frac{p_x\,\omega^x \;+\; p_y\,\omega^y}{p_y}\), die \(x\)-Achse an der Stelle \(\frac{p_x\,\omega^x \;+\; p_y\,\omega^y}{p_x}\); also jeweils dort, wo das Individuum sein gesamtes Einkommen für nur ein Gut ausgibt.

Das Individuum kann sich alle Güterbündel der Budgetmenge leisten. Von Interesse sind nur die Bündel auf der Budgetgeraden, da nur diese auch nutzenmaximal sein können. Denn für jedes Güterbündel unterhalb der Budgetgeraden gibt es Bündel auf der Budgetgeraden, die von allen Gütern mehr enthalten und somit besser sein müssen. Das Individuum gibt immer sein gesamtes Einkommen für den Konsum aus. Man darf hier nicht auf die Idee kommen, das Individuum könnte sparen wollen, um für späteren Konsum vorzusorgen. Der Konsum von Gütern zu verschiedenen Zeitpunkten ist Gegenstand der Theorie der intertemporalen Entscheidung, die hier und im Artikel zur Tauschökonomie keine Rolle spielt.

5. Die Nutzenmaximierung

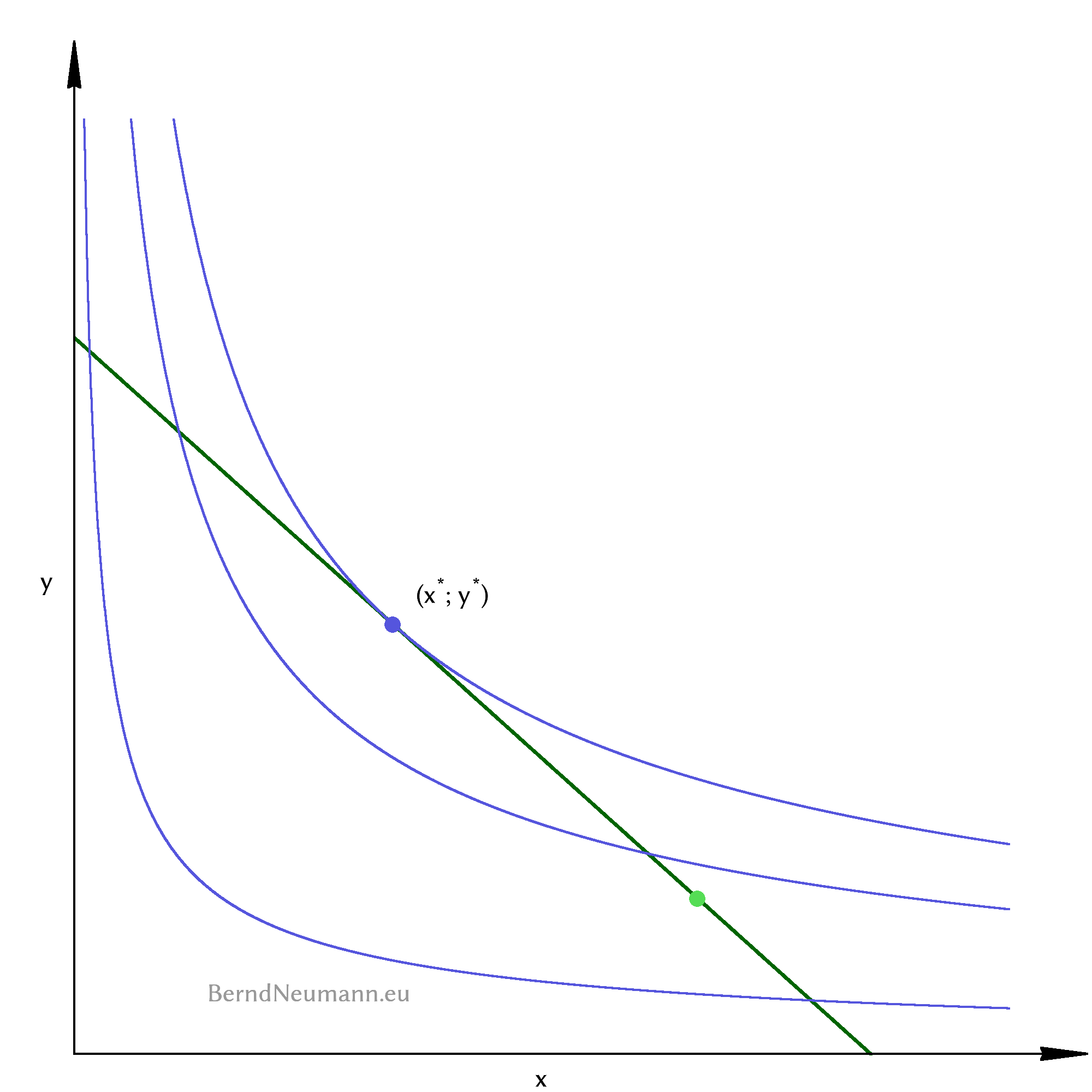
Welches Güterbündel wird der Konsument wählen? Der Antwort nähern wir uns zuerst intuitiv anhand des Diagramms in Abbildung 5. Algebraisch werden wir die Nutzenmaximierung im nächsten Abschnitt lösen.

Wählen wir innerhalb der Budgetmenge ein beliebiges Güterbündel und zeichnen die zugehörige Indifferenzkurve. Sie schneidet die Budgetgerade an zwei Punkten, so dass die Möglichkeitsmenge und die Bessermenge dieser Indifferenzkurve eine Schnittmenge bilden. Die Güterbündel dieser Schnittmenge sind sowohl erreichbar als auch besser. Daher wählen wir ein Güterbündel aus dieser Schnittmenge und zeichnen wieder die zugehörige Indifferenzkurve. Es zeigt sich ein ähnliches Bild wie zuvor, jedoch hat unser Güterbündel ein höheres Nutzenniveau und die Schnittmenge ist etwas kleiner. Diesen Vorgang wiederholen wir, bis die Schnittmenge verschwunden ist. Das ist der Fall, wenn wir ein Güterbündel auf der Budgetgeraden gewählt haben, dessen Indifferenzkurve die Budgetgerade im Punkt dieses Bündels gerade berührt. Alle anderen Güterbündel dieser Indifferenzkurve und alle Bündel ihrer Bessermenge liegen außerhalb der Budgetmenge. Dieses ist das nutzenmaximale Güterbündel, das der Konsument wählt.

6. Das Lagrange-Verfahren

Die Frage nach dem nutzenmaximalen Güterbündel ist in mathematischen Worten ein Optimierungsproblem mit Nebenbedingung. Zum Glück müssen wir dieses Problem nicht selbst lösen, weil Joseph-Louis Lagrange Mitte des 18. Jahrhunderts ein Lösungs-Verfahren erklärte. Man nennt es daher Lagrange-Verfahren. Praktisch ist, dass man die Mathematik nicht im Detail verstehen, sondern nur das Verfahren Schritt für Schritt korrekt anwenden muß, um ein solches Optimierungsproblem zu lösen.

Wir formulieren zuerst das Optimierungsproblem: Gesucht ist der maximale Wert der Nutzenfunktion \(U(x, y)\), wobei \(x\) und \(y\) aber nicht frei gewählt werden können, sondern als Nebenbedingung die Budgetrestrikton erfüllen müssen: $$\begin{aligned} &\text{max} \; U(x, y) \; = \; x^{\alpha} \, y^{1-\alpha}\\[1em] &NB: \;\; p_xx \,+\, p_yy \;\leq \; p_x\omega^x \,+\, p_y\omega^y \end{aligned}$$

1. Der erste Schritt des Lagrange-Verfahrens ist die Lagrange-Funktion aufzustellen. Sie besteht aus der Zielfunktion, zu der man die mit dem Lagrange-Multiplikator \(\lambda\) multiplizierte und nach null umgeformte Nebenbedingung addiert: $$\begin{aligned} L(x, y, \lambda) \; &= \; x^{\alpha} \, y^{1-\alpha}\\[1em]\;\;\;&+\; \lambda(p_x\,x \,+\, p_y\,y \;-\; p_x\,\omega^x \,-\, p_y\,\omega^y) \end{aligned}$$

2. Man bildet die partiellen Ableitungen der Lagrange-Funktion zu allen Variablen und Lagrange-Multiplikatoren. $$\begin{aligned} \frac{\partial L(x, y, \lambda)}{\partial x} \; &= \; \alpha x^{\alpha-1} \; y^{1-\alpha} \;+\; \lambda\,p_x\\[1em] \frac{\partial L(x, y, \lambda)}{\partial y} \; &= \; x^{\alpha} \; (1-\alpha)\,y^{1-\alpha-1} \;+\; \lambda\,p_y\\[1em] \frac{\partial L(x, y, \lambda)}{\partial \lambda} \; &= \; p_x\;x \;+\; p_y\;y\,-\,p_x\;\omega^x \;-\; p_y\;\omega^y \end{aligned}$$

Diese Ableitungen setzt man gleich null, und wir schreiben die Minuszeichen im Exponenten als Brüche: $$\begin{aligned} \frac{\alpha\,x^{\alpha}\,y}{x y^{\alpha}} \;+\; \lambda\,p_x\; &= \; 0\\[1em] \frac{(1-\alpha)\,x^{\alpha}}{y^{\alpha}} \;+\; \lambda\,p_y \; &= \; 0\\[1em] p_x\;x \;+\; p_y\;y\,-\,p_x\;\omega^x \;-\; p_y\;\omega^y \; &= \; 0 \end{aligned}$$

3. Man löst das so gewonnene Gleichungssystem. Wir eleminieren das \(\lambda\), indem wir die ersten beiden Gleichungen nach \((-\lambda)\) umformen, gleichsetzen und anschließend nach \(y\) auflösen: $$\begin{aligned} \frac{\alpha\,x^{\alpha}\,y}{x y^{\alpha}\,p_x} \; &= \; -\lambda\\[1em] \frac{(1-\alpha)\,x^{\alpha}}{y^{\alpha}\,p_y} \; &= \; -\lambda\\[1em] \frac{\alpha\,x^{\alpha}\,y}{x y^{\alpha}\,p_x} \; &= \; \frac{(1-\alpha)\,x^{\alpha}}{y^{\alpha}\,p_y}\\[1em] y \; &= \; \frac{(1-\alpha)\,x\,p_x}{\alpha\,p_y} \end{aligned}$$

Das setzen wir in die dritte Gleichung (aus \(\frac{\partial L}{\partial \lambda}\)) ein und lösen nach \(x\) auf: $$\begin{aligned} p_x\;x \;+\; p_y\;\left(\frac{(1-\alpha)\,x\,p_x}{\alpha\,p_y}\right) \; &= \; p_x\;\omega^x \;+\; p_y\;\omega^y\\[1em] p_x\;x \;+\; \frac{(1-\alpha)\,x\,p_x}{\alpha} \; &= \; p_x\;\omega^x \;+\; p_y\;\omega^y\\[1em] x \;+\; \frac{(1-\alpha)\,x}{\alpha} \; &= \; \frac{p_x\;\omega^x \;+\; p_y\;\omega^y}{p_x}\\[1em] \left(\frac{\alpha}{\alpha}+\frac{(1-\alpha)}{\alpha}\right)\,x \; &= \; \frac{p_x\;\omega^x \;+\; p_y\;\omega^y}{p_x}\\[1em] x \; &= \; \frac{\alpha\;(p_x\;\omega^x \;+\; p_y\;\omega^y)}{p_x} \end{aligned}$$

Diese Gleichung ist die Lösung des Lagrange-Verfahrens für die Variable \(x\). Sie sagt uns, welche Menge von Gut \(X\) der Konsument mit der Anfangsausstattung \((\omega^x; \omega^y)\) zu den Preisen \(p_x\) und \(p_y\) als nutzenmaximale Menge wählt. – Von Interesse ist für alles Folgende, wie sich die gewählte Gütermenge \(x\) bei verschiedenen Preisen verhält. Wir schreiben sie daher als eine Funktion in Abhängigkeit von den Preisen. Diese Funktion ist die Marshall'sche Nachfragefunktion. Um anzuzeigen, dass es sich um eine nutzenmaximale Gütermenge handelt, versehen wir sie mit einem Asterisken. Die Marshall'sche Nachfragefunktion für Gut \(Y\) erhält man analog aus dem Gleichungssystem des Lagrange-Verfahrens: $$\begin{aligned} x^*(p_x, p_y) \; &= \; \frac{\alpha\;(p_x\;\omega^x \;+\; p_y\;\omega^y)}{p_x}\\[1em] y^*(p_x, p_y) \; &= \; \frac{(1-\alpha)\;(p_x\;\omega^x \;+\; p_y\;\omega^y)}{p_y} \end{aligned}$$

Das Individuum konsumiert also das Güterbündel \((x^*; y^*)\) und maximiert so seinen Nutzen. Dabei ist unerheblich, wie hoch dieser Nutzenwert ist, denn relevant ist nur, dass dieses Güterbündel innerhalb der Budgetmenge das mit dem höchsten Nutzenwert ist. Dieses Bündel beschreiben die Marshall'schen Nachfragefunktionen, und mit ihnen ist alles Wesentliche über die Entscheidung eines einzelnen Individuums gesagt.

Soweit kam bei der Analyse nur die Entscheidung eines einzelnen Individuums vor. Man spricht von partieller Gleichgewichtsanalyse. Im Artikel zur Tauschökonomie wird es darum gehen, das gleichzeitige Handeln mehrer Individuen zu untersuchen. Man spricht dann von allgemeiner Gleichgewichtsanalyse. Ihr zentrales Konzept stelle ich im folgenden und letzten Abschnitt vor.

7. Die Edgeworth-Box

Um die Interaktion zwischen Individuen darzustellen, braucht man ein zweites Individuum und dessen Gütermengendiagramm. Das erste Individuum nennen wir \(A\), das zweite nennen wir \(B\). Die Nutzenfunktionen, Güterbündel und Marshall'schen Nachfragefunktionen versehen wir dementsprechend mit einem Index \(a\) und \(b\). Das Gütermengendiagram von \(B\) zeichnen wir aber nicht auf oder neben das Gütermengendiagramm von \(A\). Stattdessen wird das Koordinatensystem von \(B\) um 180 Grad gedreht und sein Ursprung von \(A\) aus gesehen nach rechts oben versetzt gezeichnet. So erhalten wir eine Edgeworth-Box. Sie bildet eine Ökonomie ab, in der von beiden Gütern bestimmte Mengen vorhanden sind, und jeder Punkt innerhalb der Box drückt eine bestimmte Verteilung der Güter zwischen den Individuen aus. Eine solche Verteilung wird Allokation genannt.

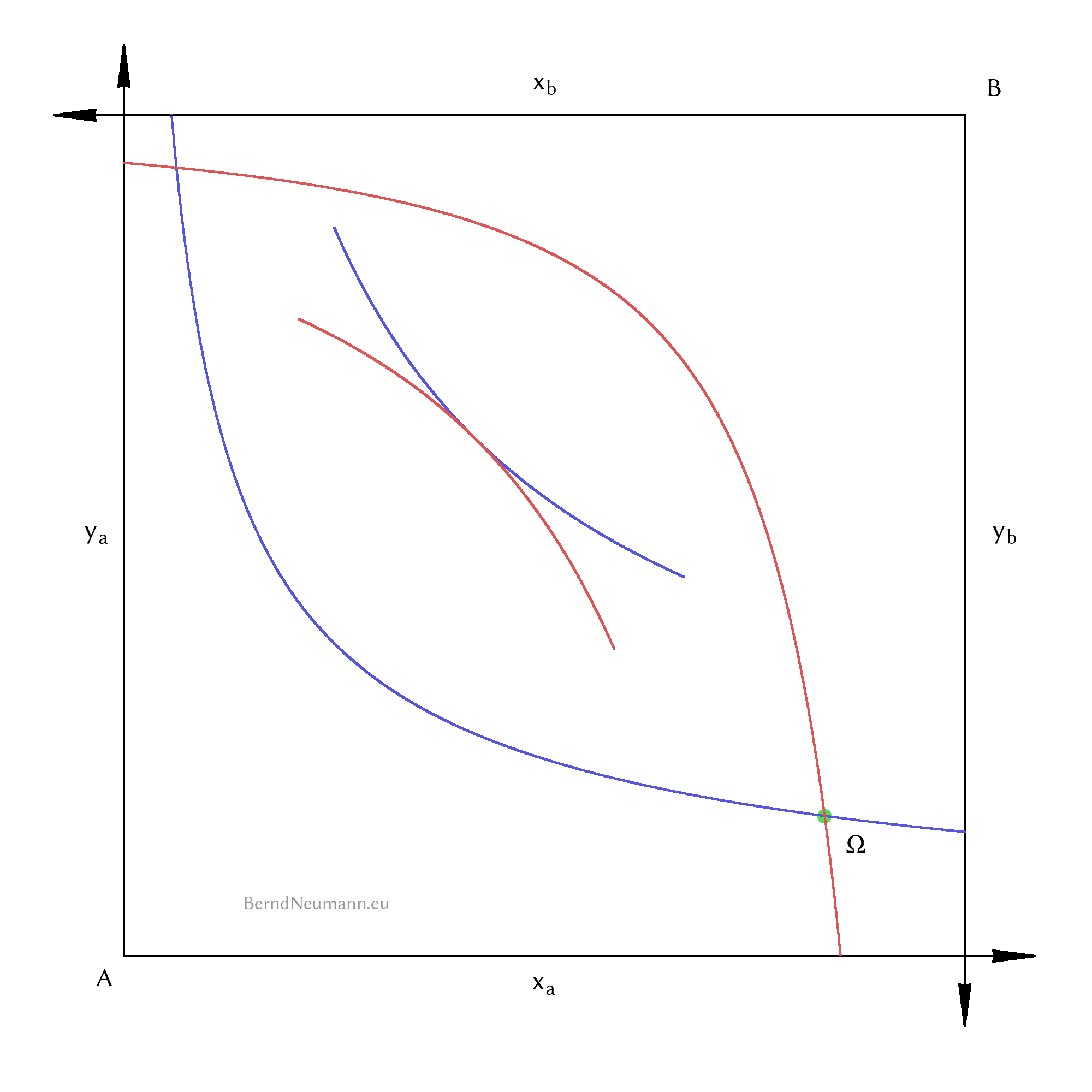
Bei einer Allokation weiter rechts in der Box hat Individuum \(A\) mehr von Gut \(X\); bei einer Allokation weiter oben mehr von Gut \(Y\). Individuum \(B\) verfügt dann über entsprechend weniger des jeweiligen Gutes. Im Punkt der Anfangsausstattung \(\Omega\) verfügt Individuum \(A\) über das Bündel \((\omega^x_a; \omega^y_a)\) und Individuum \(B\) über das Bündel \((\omega^x_b; \omega^y_b)\). Zeichnet man zu dieser Allokation die entsprechenden Indifferenzkurven, bilden ihre Bessermengen eine linsenförmige Schnittmenge als gemeinsame Bessermenge. Das bedeutet, dass Allokationen innerhalb dieser Schnittmenge für beide besser sind. Es ist also möglich, das Wohlergehen der Individuen zu verbessern, ohne dass dafür jemand an Wohlergehen verlieren müßte; und es wäre ineffizient, das nicht zu tun. Bei manchen Allokationen gibt es keine solche Schnittmenge, weil sich dort die Indifferenzkurven gerade berühren. Eine solche Allokation heißt pareto-effizient. Dort ist es nicht mehr möglich, einen besser zu stellen, ohne dass dafür der andere einen geringeren Nutzen hinnehmen müßte.

8. Schlußbemerkung

In diesem Artikel sind 16 Begriffe der Mikroökonomik vorgestellt worden. Die Darstellung ist keinesfalls ausführlich, sondern soll nur den propädeutischen Zweck erfüllen, den an fortgeschrittene Studentinnen und Studenten der Wirtschaftsschaften gerichteten Artikel über die Tauschökonomie und den Ersten Hauptsatz der Wohlfahrtökonomik einem ökonomischen Laien zugänglich zu machen. Folgende Liste zeigt die 16 Begriffe:

• Gütermengendiagramm
• Güterbündel
• Indifferenzkurve
• Bessermenge
• Nutzenfunktion
• Cobb-Douglas-Nutzenfunktion
• Grenzrate der Substitution
• Möglichkeitsmenge, Budgetmenge
• Budgetgerade, Preisgerade
• Anfangsausstattung
• Nutzenmaximierung
• Lagrange-Verfahren
• Marschall'sche Nachfragefunktion
• Edgeworth-Box
• Gemeinsame Bessermenge
• Pareto-Effizienz

Wer von jedem dieser Begriffe eine Anschauung hat, weiß alles Erforderliche, um dem Artikel Die Tauschökonomie folgen zu können. Es bleibt an dieser Stelle viel Vergnügen zu wünschen.